 Problem B. 5282. (December 2022)
Problem B. 5282. (December 2022)
B. 5282. In an acute-angled triangle \(\displaystyle ABC\), the foot of the altitude drawn from vertex \(\displaystyle A\) is \(\displaystyle T\). The projection of \(\displaystyle T\) on side \(\displaystyle AB\) is \(\displaystyle D\), and its projection on side \(\displaystyle AC\) is \(\displaystyle E\). Let \(\displaystyle F\) be the intersection of side \(\displaystyle BC\) and the circle \(\displaystyle ABE\) that is different from \(\displaystyle B\). Analogously, let \(\displaystyle G\) be the intersection of side \(\displaystyle BC\) and circle \(\displaystyle ACD\), different from \(\displaystyle C\). Show that \(\displaystyle TF=TG\).
Proposed by G. Kós, Budapest
(5 pont)
Deadline expired on January 10, 2023.
Sorry, the solution is available only in Hungarian. Google translation
1. megoldás.
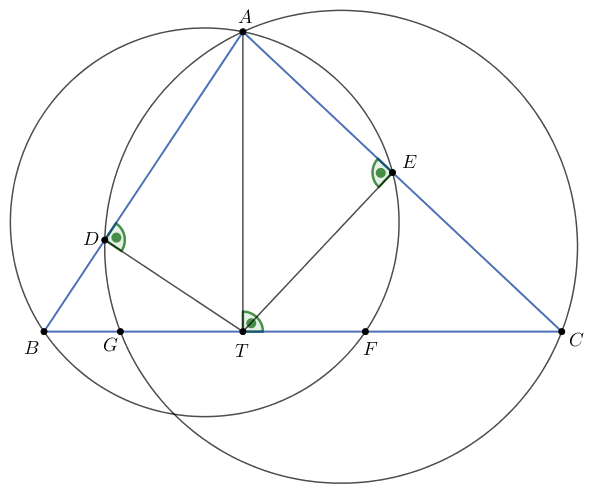
Írjuk fel az \(\displaystyle ABT\) derékszögű háromszög \(\displaystyle BT\) befogójára a befogótételt: \(\displaystyle BT^2=BA\cdot BD\). A \(\displaystyle B\) pontnak az \(\displaystyle ADGC\) körre vonatkozó hatványa \(\displaystyle BA\cdot BD=BC\cdot BG\). A kettő összehasonlításából kapjuk, hogy
$$\begin{align*} BT^2 &= BA\cdot BD = BC\cdot BG = \\ &= BC\cdot(BT-TG) = BC\cdot BT-BC\cdot TG = (BT+CT)\cdot BT-BC\cdot TG = \\ &= BT^2+BT\cdot CT-BC\cdot TG; \end{align*}$$\(\displaystyle BC\cdot TG = BT\cdot CT. \)
Hasonlóan, az \(\displaystyle ACT\) derékszögű háromszögből és a \(\displaystyle C\) pontnak az \(\displaystyle ABFE\) körre vonatkozó hatványából kapjuk, hogy
$$\begin{align*} CT^2 &= CA\cdot CE = BC\cdot CF = \\ &= BC\cdot(CT-TF) = BC\cdot CT-BC\cdot TF = (BT+CT)\cdot CT-BC\cdot TF = \\ &= CT^2+BT\cdot CT-BC\cdot TF; \end{align*}$$\(\displaystyle BC\cdot TF = BT\cdot CT. \)
Tehát,
\(\displaystyle BC\cdot TF = BT\cdot CT = BC\cdot TG, \)
\(\displaystyle TF = TG. \)
2. megoldás. Szintén az \(\displaystyle ABT\) és \(\displaystyle ACT\) háromszögekre felírt befogótételből
\(\displaystyle AB\cdot AD = AT^2 = AC\cdot AE, \)
ebből látjuk, hogy \(\displaystyle BCED\) húrnégyszög.
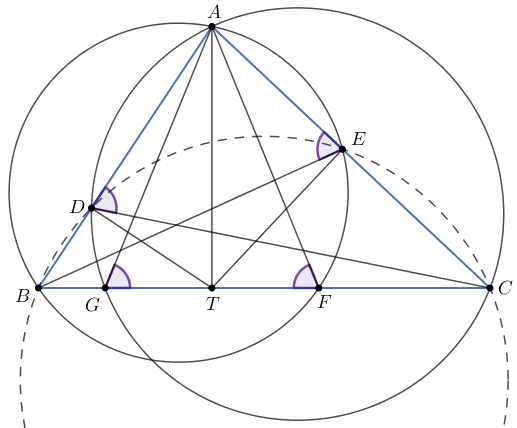
A kerületi szögek tételéből
\(\displaystyle FGA\sphericalangle = CGA\sphericalangle = CDA\sphericalangle = 180^\circ-BDC\sphericalangle = 180^\circ-BEC\sphericalangle = AEB\sphericalangle = AFB\sphericalangle = AFG\sphericalangle. \)
Tehát, az \(\displaystyle AGF\) háromszögben a \(\displaystyle G\)-nél és az \(\displaystyle F\)-nél levő szögek egyenlők, így a háromszög egyenlő szárú, \(\displaystyle TF=TG\).
Statistics:
62 students sent a solution. 5 points: Ali Richárd, Balaskó Imola, Bencz Benedek, Bodor Mátyás, Bui Thuy-Trang Nikolett, Chen JiaTong, Chrobák Gergő, Csonka Illés, Csupor Albert Dezső, Czanik Pál, Czirják Márton Pál, Diaconescu Tashi, Fehérvári Donát, Fodor Dóra, Fórizs Emma, Fülöp Csilla, Gömze Norken, Hetyei Dániel, Holló Martin, Horák Zsófia, Horváth 530 Mihály, Inokai Ádám, Juhász-Molnár Erik, Keresztély Zsófia, Kosztolányi Karina, Kovács Benedek Noel, Melján Dávid Gergő, Miklós Janka, Mizik Lóránt, Prohászka Bulcsú, Romaniuc Albert-Iulian, Sárdinecz Dóra, Seprődi Barnabás Bendegúz, Simon László Bence, Sütő Áron, Szakács Ábel, Szakács Domonkos, Szemlér Bálint, Tarján Bernát, Teveli Jakab, Tran Dávid, Tusnády Sámuel, Varga Boldizsár, Veres Dorottya, Virág Rudolf, Wiener Anna, Zhai Yu Fan, Zömbik Barnabás. 4 points: 6 students. 2 points: 3 students. 0 point: 2 students. Unfair, not evaluated: 2 solutionss.
Problems in Mathematics of KöMaL, December 2022
