Problem B. 5300. (February 2023)

B. 5300. Let \(\displaystyle T\) be a regular tetrahedron of unit edge. Inscribe a cube in \(\displaystyle T\) such that exactly two vertices of the cube lie on each face of \(\displaystyle T\), as shown in the figure (the dashed lines are parallel to the appropriate edges of the tetrahedron). What is the volume of the cube?

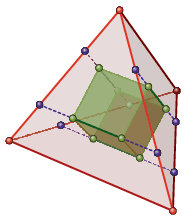
Proposed by V. Vígh, Sándorfalva

(5 pont)

Deadline expired on March 10, 2023.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. A könnyebb érthetőség érdekében helyezzük el a tetraédert egy nagy kockában a szokásos módon, és használjuk az ábra jelöléseit. A tetraéder csúcsai legyenek \(\displaystyle A\), \(\displaystyle B\), \(\displaystyle C\) és \(\displaystyle D\); a beírt kocka \(\displaystyle KLMNSTUV\) úgy, hogy az \(\displaystyle UV\), \(\displaystyle ST\), \(\displaystyle LM\) és \(\displaystyle KN\) élek rendre az \(\displaystyle ABC\), \(\displaystyle ABD\), \(\displaystyle ACD\) és \(\displaystyle BCD\) lapokra illeszkednek, továbbá az \(\displaystyle UV\) egyenes az \(\displaystyle AC\) és \(\displaystyle BC\) éleket az \(\displaystyle A_C\) és \(\displaystyle B_C\) pontokban metszi, stb.

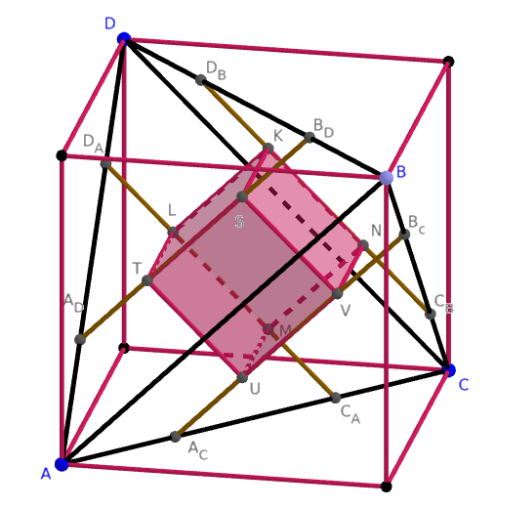
Legyen

\(\displaystyle AA_C=AA_D=BB_C=BB_D=CC_A=CC_B=DD_A=DD_B=x;\)

ekkor

\(\displaystyle A_CC_A=A_DD_A=B_DD_B=B_CC_B=1-2x.\)

Jelölje a beírt kocka élhosszát \(\displaystyle a\); valamint vegyük észre, hogy a befoglaló kocka élhossza \(\displaystyle 1/\sqrt 2\). A következőkben kifejezzük \(\displaystyle a\)-t az \(\displaystyle x\) segítségével kétféleképpen.

Először is vegyük észre, hogy az \(\displaystyle STUV\) és \(\displaystyle KLMN\) lapok párhuzamosak egymással, valamint az \(\displaystyle AB\) és \(\displaystyle CD\) kitérő élekkel, ezért a befoglaló kocka megfelelő lappárjával is. Messük el ezzel a négy párhuzamos síkkal a befoglaló kocka \(\displaystyle BD\) átlójú lapját, így a következő ábrát kapjuk.

Itt \(\displaystyle D'_BB'_D=a\) a párhuzamos lapsíkok távolsága, valamint a párhuzamos szelők tétele miatt

\(\displaystyle \frac{1-2x}{1}=\frac{B_DD_B}{BD}=\frac{B'_DD'_B}{D'B}=\frac{a}{\frac 1 {\sqrt 2}}.\)

Másrészről \(\displaystyle ACD\) szabályos háromszög és \(\displaystyle AA_C=AA_D\), ezért \(\displaystyle AA_CA_D\triangle\) is szabályos, így \(\displaystyle x=A_CA_D=a\). Ezt visszaírva az előző összefüggésbe az \(\displaystyle 1-2a=\sqrt 2 a\) egyenletet kapjuk. Ebből \(\displaystyle a=1/(2+\sqrt 2)\), és a keresett térfogat \(\displaystyle V_{kocka}=a^3=1/(2+\sqrt 2)^3\).

Statistics:

51 students sent a solution.
5 points:	Ali Richárd, Aravin Peter, Blaskovics Ádám, Bodor Mátyás, Csonka Illés, Czirják Márton Pál, Diaconescu Tashi, Domján Olivér, Fehérvári Donát, Forinyák Judit Virág, Gömze Norken, Holló Martin, Horváth 530 Mihály, Juhász-Molnár Erik, Kerekes András, Kovács Benedek Noel, Melján Dávid Gergő, Nádor Artúr, Nguyen Kim Dorka, Prohászka Bulcsú, Puppi Barna, Sárdinecz Dóra, Seprődi Barnabás Bendegúz, Szabó Imre Bence, Szakács Ábel, Szanyi Attila, Teveli Jakab, Tusnády Sámuel, Veres Dorottya, Vigh 279 Zalán, Virág Lénárd Dániel, Zhai Yu Fan, Zömbik Barnabás.
4 points:	Chrobák Gergő, Csilling Dániel, Czanik Pál, Fórizs Emma, Kocsis 827 Péter, Tran Dávid, Varga Boldizsár, Virág Rudolf.
3 points:	1 student.
2 points:	1 student.
1 point:	5 students.
0 point:	1 student.

Problems in Mathematics of KöMaL, February 2023