Problem B. 5330. (September 2023)

B. 5330. Suppose that \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\) is a primitive Pythagorean triple, i.e., \(\displaystyle a\), \(\displaystyle b\) and \(\displaystyle c\) are relatively prime positive integers satisfying \(\displaystyle a^2+b^2=c^2\). Show an axially symmetrical polygon that can be decomposed into \(\displaystyle c\) right-angled triangles with sides \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\).

Proposed by G. Kós, Budapest

(5 pont)

Deadline expired on October 10, 2023.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Jól ismert, hogy \(\displaystyle a\) és \(\displaystyle b\) közül az egyik páratlan, a másik páros; mivel a feladatban \(\displaystyle a\) és \(\displaystyle b\) szerepe szimmetrikus, az általánosság csorbítása nélkül feltehetjük, hogy \(\displaystyle b\) páros. A pitagoraszi számhármasok jól ismert előállítása szerint alkalmas \(\displaystyle s>t\) pozitív egészekkel \(\displaystyle a=s^2-t^2\), \(\displaystyle b=2st\) és \(\displaystyle c=s^2+t^2\).

Állítsunk össze \(\displaystyle s^2\), illetve \(\displaystyle t^2\) darab, \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\) oldalú kis háromszögből egy \(\displaystyle sa\), \(\displaystyle sb\), \(\displaystyle sc\), illetve egy \(\displaystyle ta\), \(\displaystyle tb\), \(\displaystyle tc\) oldalú nagyobb háromszöget, ezekből összeilleszthetjük az ábrán látható \(\displaystyle ABCD\) konkáv négyszöget.

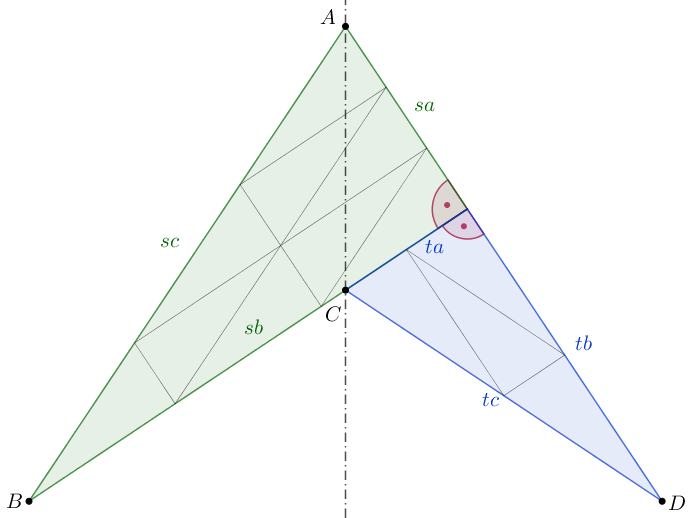
A négyszögnek két-két szomszédos oldala egyenlő:

\(\displaystyle AD = sa+tb = s(s^2-t^2)+t\cdot 2st +s(s^2+t^2) = sc = AB \)

és

\(\displaystyle BC = sb-ta = s\cdot 2st-t(s^2-t^2) = t(s^2+t^2) = tc =CD; \)

az így kapott négyszög tehát egy deltoid, ami szimmetrikus az \(\displaystyle AC\) átlójára.

A felhasznált kis háromszögek száma pontosan \(\displaystyle s^2+t^2=c\).

Statistics:

65 students sent a solution.
5 points:	Ali Richárd, Bodor Mátyás, Chen JiaTong, Fórizs Emma, Holló Martin, Kocsis 827 Péter, Kovács Benedek Noel, Pálfi András, Petrányi Lilla, Prohászka Bulcsú, Sánta Gergely Péter, Sárdinecz Dóra, Szakács Ábel, Tran Dávid, Veres Dorottya, Zhai Yu Fan, Zömbik Barnabás.
4 points:	Virág Tóbiás.
2 points:	3 students.
1 point:	1 student.
0 point:	35 students.
Not shown because of missing birth date or parental permission:	6 solutions.

Problems in Mathematics of KöMaL, September 2023