Problem B. 5337. (October 2023)

B. 5337. A regular triangle is drawn over each side of a regular \(\displaystyle n\)-gon, on the outside. The third vertices of the triangles form a larger \(\displaystyle n\)-gon. What may the number \(\displaystyle n\) be if the ratio of the areas of the two polygons is an integer?

Proposed by B. Hujter, Budapest

(4 pont)

Deadline expired on November 10, 2023.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Jelölje \(\displaystyle A_1 A_2 A_3 \ldots A_{n-1} A_n\) az eredeti (kisebb) szabályos \(\displaystyle n\)-szöget, és jelölje \(\displaystyle B_i\) az \(\displaystyle A_iA_{i+1}\) oldalra rajzolt szabályos háromszög harmadik csúcsát, így a nagyobb szabályos \(\displaystyle n\)-szög \(\displaystyle B_1 B_2 B_3 \ldots b_{n-1} B_n\).

Jelölje a kisebbik szabályos \(\displaystyle n\)-szög oldalhosszát \(\displaystyle a\), a nagyobbikét \(\displaystyle b\). Mivel a két szabályos \(\displaystyle n\)-szög hasonló, ezért területük aránya \(\displaystyle \dfrac{b^2}{a^2}\).

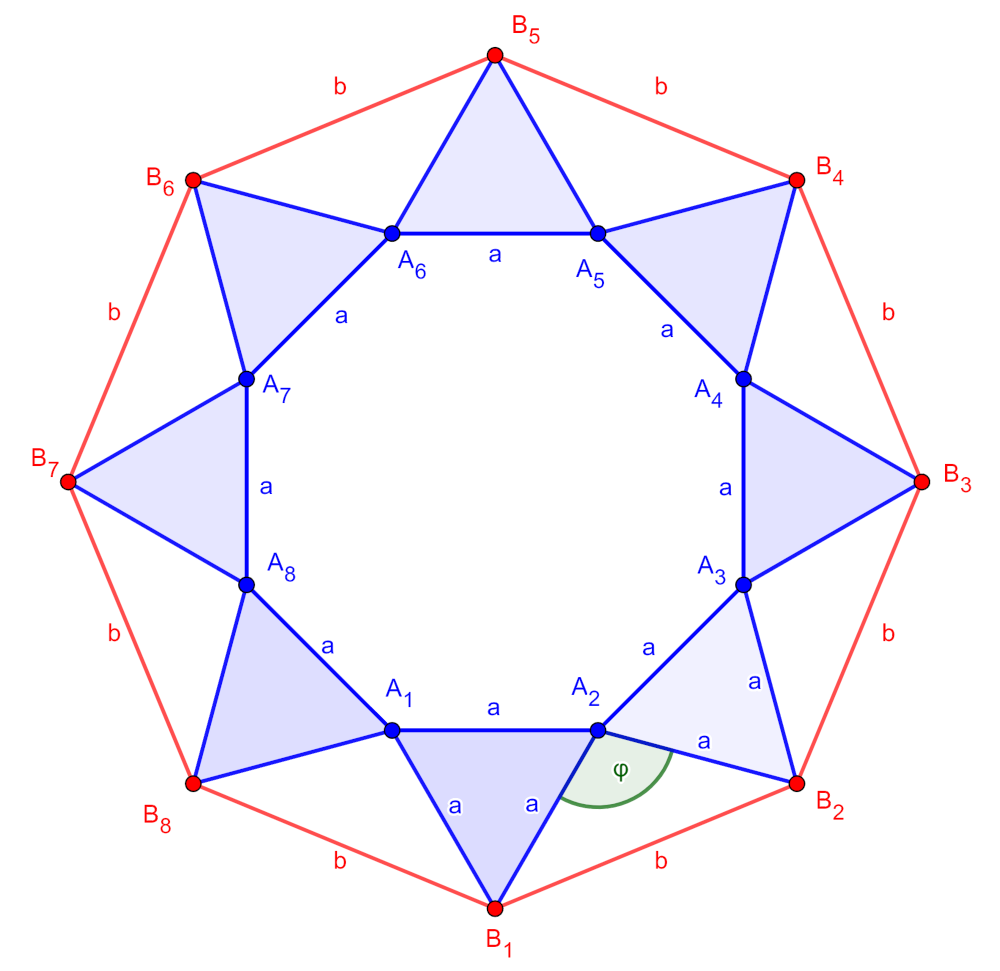
Tekintsük az \(\displaystyle A_1A_2B_1\) egyenlő szárú háromszöget. Jelölje \(\displaystyle \varphi\) a két \(\displaystyle a\) hosszúságú oldala által bezárt szöget. Mivel a szabályos \(\displaystyle n\)-szög egy belső szöge \(\displaystyle \frac{n-2}{n} \cdot 180^{\circ}\), ezért \(\displaystyle \varphi = 360^{\circ} - \frac{n-2}{n} \cdot 180^{\circ} - 2 \cdot 60^{\circ} = 60^{\circ} + \frac{360^\circ}{n}\).

Ha \(\displaystyle n=3\), akkor \(\displaystyle \varphi = 180^{\circ}\), ilyenkor az \(\displaystyle A_1A_2B_1\) háromszög egy szakasszá fajul.

\(\displaystyle n > 3\) esetén \(\displaystyle 60^{\circ} < \varphi < 180^{\circ}\), így az \(\displaystyle A_1A_2B_1\) háromszög tényleg létezik (méghozzá az ábrán látható elrendezésben: a nagyobb szabályos \(\displaystyle n\)-szög tartalmazza, míg a kisebbik szabályos \(\displaystyle n\)-szög nem tartalmazza az \(\displaystyle A_1A_2B_1\) háromszöget).

Felírhatjuk a koszinusztételt (az egyenlet \(\displaystyle \varphi = 180^{\circ}\) esetben is teljesül):

\(\displaystyle b^2 = a^2 + a^2 - 2a^2 \cos \varphi, \)

azaz

\(\displaystyle \frac{b^2}{a^2} = 2 - 2 \cos \varphi. \)

Így a két terület aránya pontosan akkor lesz egész, ha \(\displaystyle \cos \varphi\) egy egész szám fele. Mivel \(\displaystyle 60^{\circ} < \varphi \le 180^{\circ}\), ezért \(\displaystyle \cos \varphi\) a \(\displaystyle \left[-1,\frac12 \right)\) intervallumból vehet fel értékeket, így a következő értékek jöhetnek szóba:

\(\displaystyle \cos \varphi_1 = -1, \quad \cos \varphi_2 = -\frac12 \quad \text{és} \quad \cos \varphi_3 = 0 \quad \)

Már korábban láttuk, hogy az \(\displaystyle n_1 = 3\) esetben lesz \(\displaystyle \cos \varphi_1 = \cos 180^{\circ} = -1\), ilyenkor a két szabályos 3-szög területének aránya \(\displaystyle \frac{b^2}{a^2} = 2 - 2 \cos \varphi_1 = 4\).

Ha \(\displaystyle \cos \varphi_2 = -\frac12\), akkor \(\displaystyle \varphi_2 = 120^{\circ} = 60^{\circ} + \frac{360^\circ}{n_2}\), azaz \(\displaystyle n_2 = 6\). A két szabályos 6-szög területének aránya \(\displaystyle \frac{b^2}{a^2} = 2 - 2 \cos \varphi_2 = 3\).

Ha \(\displaystyle \cos \varphi_3 = 0\), akkor \(\displaystyle \varphi_3 = 90^{\circ} = 60^{\circ} + \frac{360^\circ}{n_1}\), azaz \(\displaystyle n_1 = 12\). A két szabályos 12-szög területének aránya \(\displaystyle \frac{b^2}{a^2} = 2 - 2 \cos \varphi_3 = 2\).

Összefoglalva: \(\displaystyle n \in \{ 3,6,12 \}\) esetén lesz a két sokszög területének aránya egész szám.

Statistics:

121 students sent a solution.
4 points:	76 students.
3 points:	16 students.
2 points:	9 students.
1 point:	5 students.
0 point:	4 students.
Not shown because of missing birth date or parental permission:	5 solutions.

Problems in Mathematics of KöMaL, October 2023