Problem B. 5351. (December 2023)

B. 5351. Let \(\displaystyle P\) be an arbitrary point inside the equilateral triangle \(\displaystyle ABC\). The line parallel to \(\displaystyle AB\) through \(\displaystyle P\) intersects sides \(\displaystyle BC\) and \(\displaystyle AC\) in points \(\displaystyle C_1\) and \(\displaystyle C_2\), respectively. Similarly, the parallel through point \(\displaystyle P\) with side \(\displaystyle BC\) intersects sides \(\displaystyle AC\) and \(\displaystyle AB\) in points \(\displaystyle A_1\) and \(\displaystyle A_2\), respectively. Finally, let the parallel through point \(\displaystyle P\) with side \(\displaystyle AC\) intersect sides \(\displaystyle AB\) and \(\displaystyle BC\) in points \(\displaystyle B_1\) and \(\displaystyle B_2\), respectively. Prove that the areas of triangles \(\displaystyle A_1B_1C_1\) and \(\displaystyle A_2B_2C_2\) are equal.

Submitted by Viktor Vígh, Sándorfalva

(3 pont)

Deadline expired on January 10, 2024.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Legyen az \(\displaystyle ABC\) háromszög oldala egységnyi, a párhuzamosok által az oldalakból levágott szakaszok az \(\displaystyle AB\), \(\displaystyle BC\), \(\displaystyle CA\) oldalakkal húzott párhuzamosok esetében rendre \(\displaystyle BC_1=AC_2=x\), \(\displaystyle C_1C=C_2C=1-x\), \(\displaystyle CA_1=BA_2=y\), \(\displaystyle A_1A=A_2A=1-y\), \(\displaystyle AB_1=CB_2=z\), \(\displaystyle B_1B=B_2B=1-z\) az ábra szerint.

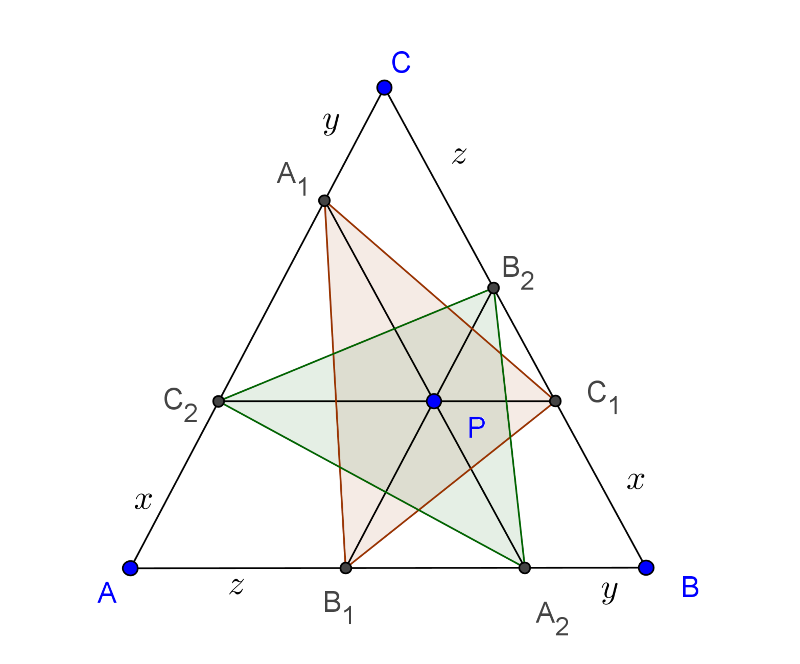
A két háromszög területének egyenlőségéhez megmutatjuk, hogy az \(\displaystyle ABC\) háromszögnek az \(\displaystyle A_1B_1C_1\) és \(\displaystyle A_2B_2C_2\) háromszögön kívül eső részei, a három-három ,,levágott" háromszög területének összege megegyezik. Ezek területének gyors kiszámítása lehetséges, mert a \(\displaystyle 60^\circ\)-os szöget közrefogó oldalak bármelyikéhez húzott magasság a háromszögből egy félszabályos háromszöget vág le, amelynek hossza így a másik oldal \(\displaystyle \frac{\sqrt{3}}{2}\)-szöröse. (Számolhatunk trigonometrikus területképlettel is.) A területek összegéből ennek megfelelően a \(\displaystyle \frac{\sqrt{3}}{4}\) kiemelhető és

\(\displaystyle T(A_1B_1C_1)=\frac{\sqrt{3}}{4}\left[(1-x)y+(1-y)z+(1-z)x\right]=\frac{\sqrt{3}}{4}(x+y+z-xy-yz-zx).\)

Ezzel teljesen megegyező módszerrel

\(\displaystyle T(A_2B_2C_2)=\frac{\sqrt{3}}{4}\left[(1-y)x+(1-x)z+(1-z)y\right]=\frac{\sqrt{3}}{4}(x+y+z-xy-yz-zx).\)

A két terület megegyezik.

Megjegyzés: Az \(\displaystyle ABC\) háromszögről nem szükséges feltenni, hogy szabályos. Tetszőleges háromszögre teljesül, hogy a feladatban leírt módon képzett két háromszög területe megegyezik. Ennek belátásához affinitással transzformáljuk a háromszöget szabályos háromszögbe, és ezzel visszavezetjük a problémát a már megoldott feladatra.

Statistics:

137 students sent a solution.
3 points:	101 students.
2 points:	17 students.
1 point:	3 students.
0 point:	1 student.
Unfair, not evaluated:	2 solutionss.
Not shown because of missing birth date or parental permission:	9 solutions.

Problems in Mathematics of KöMaL, December 2023