Problem B. 5362. (January 2024)

B. 5362. In triangle \(\displaystyle ABC\) it is given that \(\displaystyle \angle BAC=50^\circ\) and \(\displaystyle \angle ABC=70^\circ\). On sides \(\displaystyle AC\) and \(\displaystyle BC\) points \(\displaystyle E\) and \(\displaystyle D\) are chosen satisfying the following properties: \(\displaystyle \angle ABE =\angle BAD = 30^\circ\). Let \(\displaystyle M\) denote the intersection point of line segments \(\displaystyle AD\) and \(\displaystyle BE\). Find the magnitude of angles \(\displaystyle \angle ACM\) and \(\displaystyle \angle BED\).

Proposed by Sándor Róka, Nyíregyháza

(4 pont)

Deadline expired on February 12, 2024.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Használjuk az alábbi ábrát!

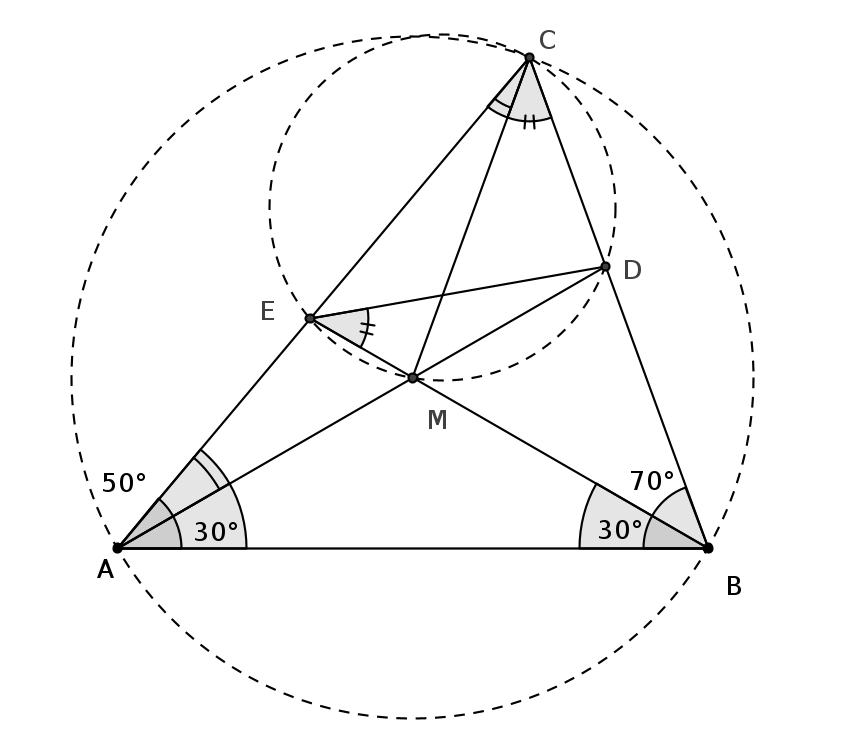
Mivel \(\displaystyle BAC\sphericalangle=50^\circ\) és \(\displaystyle ABC\sphericalangle=70^\circ\), a háromszög harmadik szöge \(\displaystyle ACB\sphericalangle=60^\circ\), és így \(\displaystyle ECD\sphericalangle=60^\circ\). Az \(\displaystyle ABM\) egyenlő szárú háromszögben \(\displaystyle AMB\sphericalangle=120^\circ\), és így ezen szög csúcsszögére, a \(\displaystyle DME\sphericalangle\)-re is teljesül, hogy a nagysága \(\displaystyle 120^\circ\). Azaz a \(\displaystyle DCEM\) négyszög két szemközti (\(\displaystyle C\)-nél és \(\displaystyle M\)-nél) lévő szögének összege \(\displaystyle 180^{\circ}\), vagyis \(\displaystyle DCEM\) húrnégyszög és köré kör rajzolható.

Az \(\displaystyle ABM\) egyenlő szárú háromszög \(\displaystyle M\) csúcsa mint középpont körül írjunk \(\displaystyle MA = MB\) sugarú kört. \(\displaystyle AMB \sphericalangle =120^{\circ}\) az \(\displaystyle AB\) (rövidebb) ívhez tartozó középponti szög a körben, ezért a \(\displaystyle BA\) (hosszabbik) látószögkörív pontosan azon \(\displaystyle P\) pontokat tartalmazza a síkon, emelyekre \(\displaystyle APB \sphericalangle = 60^{\circ}\); azaz a \(\displaystyle C\) pont rajta van ezen a körön (és így \(\displaystyle M\) az \(\displaystyle ABC\) köré írt körének a középpontja).

Az \(\displaystyle AMC\) egyenlő szárú háromszögben \(\displaystyle \underline{ACM \sphericalangle} = CAM \sphericalangle = 50^{\circ} - 30^{\circ}=\underline{20^{\circ}}\), továbbá \(\displaystyle MCB \sphericalangle = MBC \sphericalangle = 70^{\circ} - 30^{\circ}=40^{\circ}\), és így nyilván \(\displaystyle MCD \sphericalangle =40^{\circ}\).

\(\displaystyle DCEM\) köré írt körében \(\displaystyle MED \sphericalangle\) és \(\displaystyle MCD \sphericalangle\) egyaránt a (rövidebb) \(\displaystyle MD\) ívhez tartozó kerületi szög, így \(\displaystyle MED \sphericalangle= MCD \sphericalangle = 40^{\circ}\). Mivel \(\displaystyle BED \sphericalangle= MED \sphericalangle\), így \(\displaystyle \underline{BED \sphericalangle= 40^{\circ}}\).

Azaz a kérdéses szögek: \(\displaystyle ACM\sphericalangle = 20^{\circ}\) és a \(\displaystyle BED\sphericalangle = 40^{\circ}\).

Statistics:

105 students sent a solution.
4 points:	76 students.
3 points:	8 students.
2 points:	11 students.
1 point:	2 students.
Not shown because of missing birth date or parental permission:	3 solutions.

Problems in Mathematics of KöMaL, January 2024