Problem B. 5363. (January 2024)

B. 5363. Square \(\displaystyle ABCD\) is the base of a right square pyramid, and point \(\displaystyle E\) is its apex. Let \(\displaystyle F\) be the midpoint of lateral edge \(\displaystyle CE\), and let point \(\displaystyle H\) be the trisection point of lateral edge \(\displaystyle BE\) closer to point \(\displaystyle B\). Find the ratio of the volumes of the two parts created by plane \(\displaystyle AHF\) in pyramid \(\displaystyle ABCDE\).

Proposed by Géza Kiss, Csömör

(5 pont)

Deadline expired on February 12, 2024.

Sorry, the solution is available only in Hungarian. Google translation

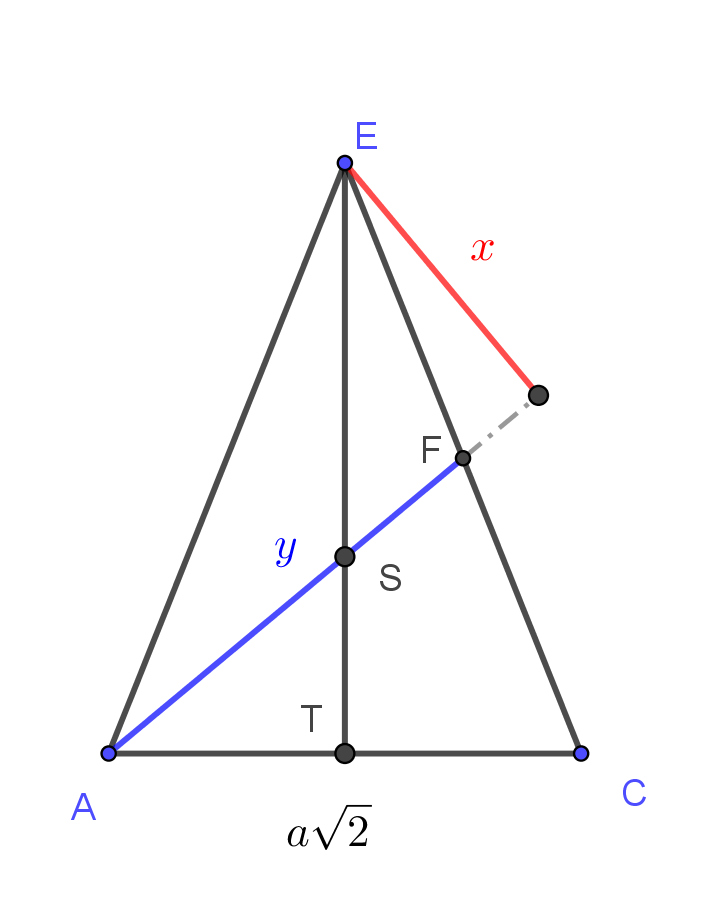
Megoldás. Jelöljük az \(\displaystyle AHF\) sík és a \(\displaystyle DE\) él metszéspontját \(\displaystyle G\)-vel, a gúla magasságának talppontját pedig \(\displaystyle T\)-vel. Először azt fogjuk megvizsgálni, hogy a \(\displaystyle G\) pont milyen arányban osztja ketté a \(\displaystyle DE\) élt. Ennek érdekében először tekintsük a gúla \(\displaystyle ACE\) síkmetszetét.

Ez egy egyenlő szárú háromszög, amelyben \(\displaystyle AF\) az \(\displaystyle EC\) szárhoz tartozó súlyvonal. Ez a súlyvonal az alaphoz tartozó magasságot – és egyben súlyvonalat – a háromszög \(\displaystyle S\) súlypontjában metszi. A súlypont harmadolja az \(\displaystyle ET\) súlyvonalat.

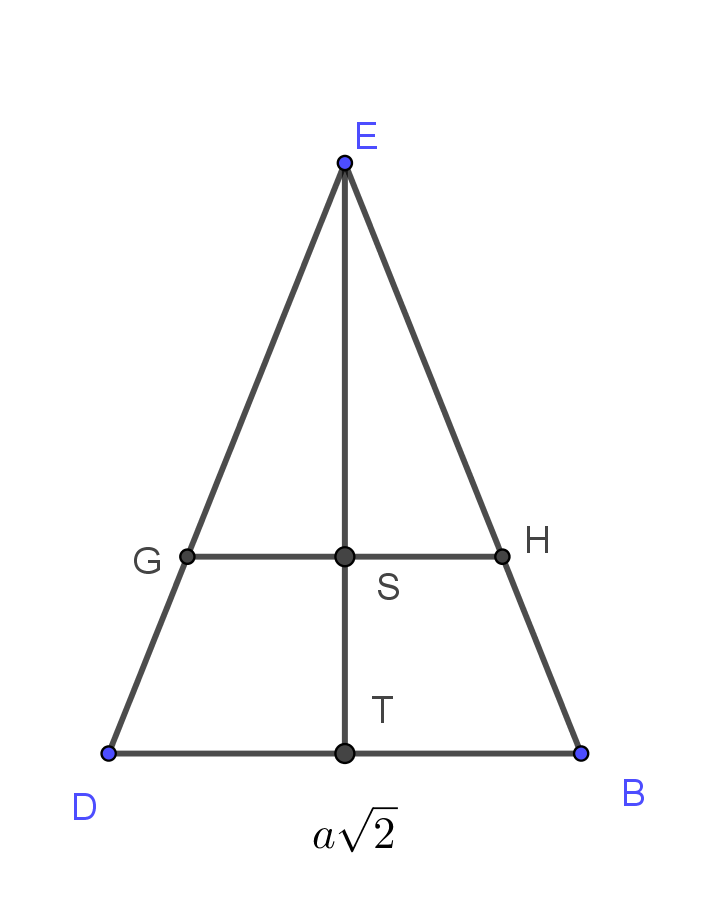
A folytatáshoz vegyük a \(\displaystyle BDE\) síkmetszetet. Ez az előbbivel egybevágó egyenlő szárú háromszög.

Ebben a háromszögben a \(\displaystyle H, G\) és \(\displaystyle S\) pontok egy egyenesbe esnek, \(\displaystyle H\) a szárat, \(\displaystyle S\) pedig az alaphoz tartozó magasságot harmadolja, így \(\displaystyle HS\) párhuzamos a \(\displaystyle BD\) alappal, vagyis a másik szárat, \(\displaystyle DE\)-t is harmadolja.

A \(\displaystyle GH\) szakasz merőleges az \(\displaystyle ACE\) síkra, tehát az \(\displaystyle AF\) szakaszra is, vagyis az \(\displaystyle AHFG\) négyszög deltoid.

A továbbiakban jelöljük az eredeti gúla alapélének hosszát \(\displaystyle a\)-val, magasságát \(\displaystyle M\)-mel, az \(\displaystyle AHFGE\) gúla magaságát \(\displaystyle x\)-szel, az \(\displaystyle AF\) szakasz hosszát \(\displaystyle y\)-nal.

Az \(\displaystyle ABCDE\) gúla térfogata \(\displaystyle V=\frac{1}{3}a^2M\). Számítsuk ki a \(\displaystyle AHFGE\) gúla térfogatát. Alaplapja deltoid, amelynek egyik átlója \(\displaystyle AF=y\), erre merőleges másik átlója a \(\displaystyle HG\) szakasz. A gúla magassága az \(\displaystyle ACE\) síkra vonatkozó szimmetria miatt egyben az \(\displaystyle AFE\) háromszög \(\displaystyle AF\)-hez tartozó magassága is. Az \(\displaystyle y\) ennek a háromszögnek súlyvonala, így az \(\displaystyle AFE\) háromszög területe fele az \(\displaystyle ACE\) háromszög területének. A jelölésekkel egyrészt

\(\displaystyle AF\cdot x=\frac{1}{2}AC\cdot M=\frac{aM\sqrt{2}}{2}.\)

Másrészt \(\displaystyle H\) és \(\displaystyle G\) harmadolópontok, ezért \(\displaystyle HG=\frac{2}{3}a\sqrt{2}\). Innen az \(\displaystyle AHFGE\) gúla térfogata

\(\displaystyle V_{AHFGE}=\frac{1}{3}\frac{y\cdot HG\cdot x}{2}=\frac{1}{6}\frac{aM\sqrt{2}}{2}\cdot \frac{2}{3}a\sqrt{2}=\frac{1}{9}a^2M=\frac{1}{3}V_{ABCDE}.\)

A megadott sík \(\displaystyle 1:2\) arányban osztja ketté a gúla térfogatát.

Statistics:

52 students sent a solution.
5 points:	Ali Richárd, Aravin Peter, Bencze Mátyás, Blaskovics Ádám, Bodor Mátyás, Bui Thuy-Trang Nikolett, Christ Miranda Anna, Csonka Illés, Csupor Albert Dezső, Deák Boldizsár Tamás, Diaconescu Tashi, Erdélyi Kata, Fórizs Emma, Gyenes Károly, Holló Martin, Horák Zsófia, Juhász-Molnár Erik, Kovács Benedek Noel, Ligeti Ábel, Petrányi Lilla, Pletikoszity Martin, Prohászka Bulcsú, Puppi Barna, Romaniuc Albert-Iulian, Sárdinecz Dóra, Sütő Áron, Szabó 721 Sámuel, Szakács Ábel, Veres Dorottya, Vigh 279 Zalán, Virág Tóbiás.
4 points:	Forrai Boldizsár, Gömze Norken, Hodossy Réka, Keresztély Zsófia, Kővágó Edit Gréta, Odabas Zeki, Sha Jingyuan, Varga 511 Vivien, Wágner Márton, Zhai Yu Fan.
3 points:	4 students.
2 points:	2 students.
1 point:	3 students.
0 point:	2 students.

Problems in Mathematics of KöMaL, January 2024