 Problem B. 5367. (February 2024)
Problem B. 5367. (February 2024)
B. 5367. \(\displaystyle a)\) In the open unit disk we place two open line segments of length \(\displaystyle \ell\) with no common points, perpendicularly to each other. What can be the value of \(\displaystyle \ell\)?
\(\displaystyle b)\) In the open unit ball we place three line segments of length \(\displaystyle \ell\) such that any two are disjoint (have no common points) and perpendicular to each other. What can be the value of \(\displaystyle \ell\)?
Proposed by Vígh Viktor, Sándorfalva
(4 pont)
Deadline expired on March 11, 2024.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Nyilvánvalóan mindkét esetben \(\displaystyle 0<\ell<2\), hiszen sem a kör, sem a gömb nem tartalmaz az átmérőjénél hosszabb szakaszt, \(\displaystyle \ell=2\) esetén pedig a szakaszok a kör, ill. a gömb középpontjában metszenék egymást.
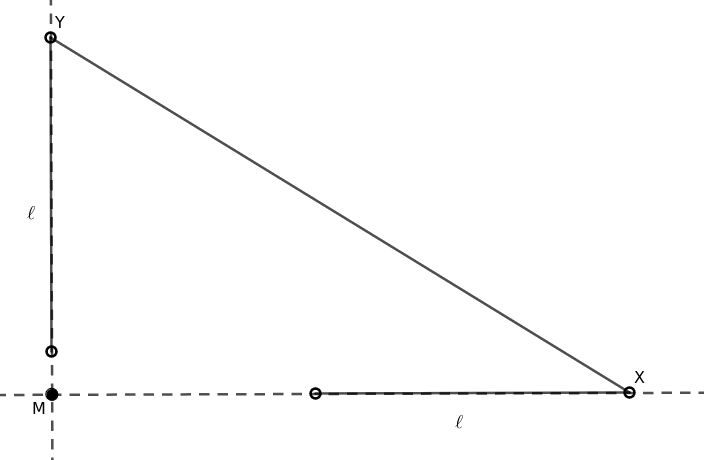
Most rátérünk az a) részre. Legyen a szakaszok tartóegyeneseinek metszéspontja \(\displaystyle M\). Először tegyük fel, hogy \(\displaystyle M\) nem illeszkedik egyik szakaszra sem. Legyenek a szakaszoknak az \(\displaystyle M\)-től távolabbi végpontjai \(\displaystyle X\), illetve \(\displaystyle Y\). Ekkor \(\displaystyle MXY\) egy derékszögű háromszög, amelynek derékszögű csúcsa \(\displaystyle M\), és amelynek mindkét befogója legalább \(\displaystyle \ell\) hosszúságú. A Pitagorasz-tételből következik, hogy \(\displaystyle XY\ge \ell \sqrt2\). Másrészt a feltételek szerint \(\displaystyle X\)-t és \(\displaystyle Y\)-t a körlap lezártja tartalmazza, ezért \(\displaystyle XY\le 2\). Ezekből \(\displaystyle \ell \le \sqrt 2\) adódik.
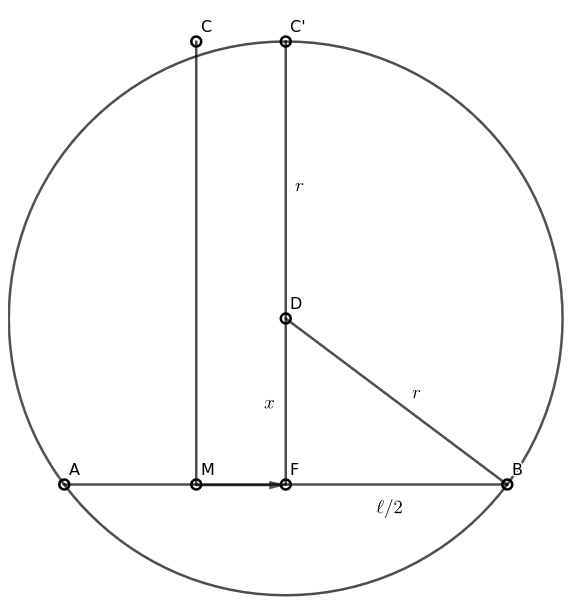
Most tegyük fel, hogy \(\displaystyle M\) az elhelyezett \(\displaystyle AB\) szakasz egy pontja, a másik szakasz \(\displaystyle M\)-től távolabbi végpontja legyen \(\displaystyle C\). Világos, hogy a második szakaszt \(\displaystyle M\) irányába eltolva a körön belül marad, ezért feltehető, hogy a második szakasz éppen \(\displaystyle MC\). A feltételek szerint az \(\displaystyle ABC\) háromszög körülírt körének sugara legfeljebb egységnyi.
Legyen \(\displaystyle AB\) felezőpontja \(\displaystyle F\), és toljuk el \(\displaystyle C\) pontot \(\displaystyle \overrightarrow{MF}\)-ral, így kapjuk \(\displaystyle C'\) pontot. Világos, hogy az \(\displaystyle ABC'\) háromszöget is tartalmazza az \(\displaystyle ABC\) háromszög körülírt köre (hiszen a \(\displaystyle C\) pont \(\displaystyle C'F\)-re vonatkozó tükörképe rajta van a körvonalon), ezért \(\displaystyle ABC'\) körülírt körének sugara is legfeljebb egységnyi. Másrészről \(\displaystyle ABC'\) körülírt körének sugara kifejezhető \(\displaystyle \ell\) segítségével; az ábra szerint \(\displaystyle (\ell/2)^2+x^2=r^2\) és \(\displaystyle x+r=\ell\). Ebből \(\displaystyle x=\ell-r\)-t visszahelyettesítve \(\displaystyle r=5\ell/8\) adódik. Innen \(\displaystyle r\le 1\) észrevételünk miatt \(\displaystyle \ell\le 8/5\).
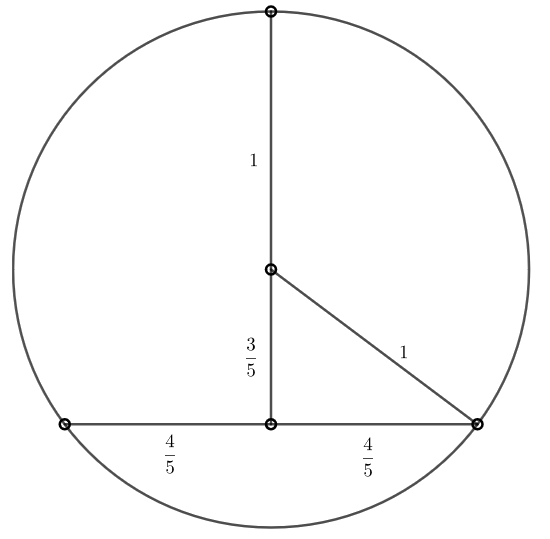
Mindkét vizsgált esetben teljesül tehát, hogy \(\displaystyle \ell\le 8/5\). Könnyen látható, hogy az ábra szerinti elrendezésben \(\displaystyle \ell=8/5\) megvalósítható. Továbbá a szakaszokat a megfelelő arányban kicsinyítve a középpontjaikból minden \(\displaystyle 0<\ell<8/5\) is megvalósítható. Ezért az a) esetben \(\displaystyle 0<\ell\le 8/5\).
Rátérünk a b) részre; megmutatjuk, hogy itt minden \(\displaystyle 0<\ell<2\) lehetséges. Rögzítsünk egy \(\displaystyle 0<\ell<2\) értéket, legyen
\(\displaystyle 0<d=\sqrt{1-(\ell/2)^2}<1, \)
és helyezzük el a gömbünket a térbeli derékszögű koordinátarendszerben úgy, hogy közzépontja az origóba essen.
Tekintsük most az \(\displaystyle xy\)-síkban az \(\displaystyle x=d\) egyenletű egyenest, az \(\displaystyle yz\)-síkban az \(\displaystyle y=d\) egyenest; és az \(\displaystyle xz\)-síkban a \(\displaystyle z=d\) egyenletű egyenest. Ezek páronként egymásra merőleges, kitérő egyenesek, amelyek a nyílt gömböt egy-egy nyílt, \(\displaystyle \ell\) hosszúságú (és szükségképpen páronként idegen) szakaszban metszik. Ez a példa mutatja, hogy valóban minden \(\displaystyle 0<\ell<2\) lehetséges.
Statistics:
105 students sent a solution. 4 points: 56 students. 3 points: 8 students. 2 points: 25 students. 1 point: 2 students. 0 point: 10 students. Not shown because of missing birth date or parental permission: 3 solutions.
Problems in Mathematics of KöMaL, February 2024
