Problem B. 5369. (February 2024)

B. 5369. Inside an equilateral triangle \(\displaystyle ABC\), point \(\displaystyle P\) is chosen such that \(\displaystyle \angle APB=150^\circ\). Prove that \(\displaystyle {PA^2+PB^2=PC^2}\).

Proposed by Viktor Vígh, Sándorfalva

(4 pont)

Deadline expired on March 11, 2024.

Sorry, the solution is available only in Hungarian. Google translation

1. megoldás. Használjuk az alábbi ábrát és jelöléseit!

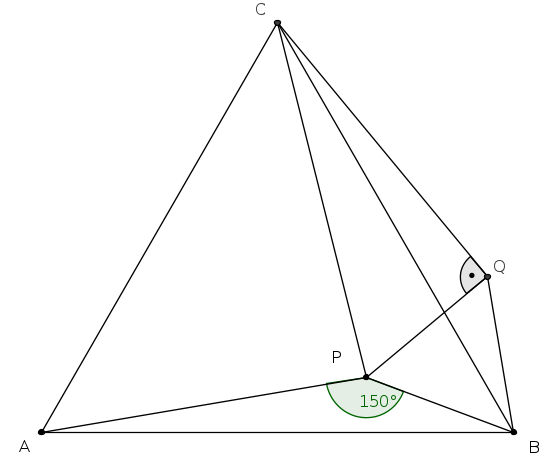
Az \(\displaystyle APB\) háromszöget forgassuk el a \(\displaystyle B\) pont körül \(\displaystyle -60^{\circ}\)-kal. Ekkor az \(\displaystyle A\), \(\displaystyle P\) és \(\displaystyle B\) pont képe rendre \(\displaystyle C=A'\), \(\displaystyle Q=P'\) és \(\displaystyle B=B'\). A forgatás távolság- és szögtartása miatt \(\displaystyle BQ=B'P'=BP\), és \(\displaystyle CQB \sphericalangle = A'P'B' \sphericalangle = APB \sphericalangle = 150^{\circ}\). Továbbá, mivel \(\displaystyle 60^{\circ}\)-kal forgattunk, \(\displaystyle PBQ \sphericalangle = PBP' \sphericalangle = 60^{\circ}\). Azaz a \(\displaystyle PBQ\) háromszög egyenlő szárú és \(\displaystyle 60^{\circ}\)-os szögű, vagyis szabályos. Emiatt \(\displaystyle PQC \sphericalangle = 150^{\circ} - 60^{\circ} = 90^{\circ}\), azaz a \(\displaystyle PQC\) háromszög derékszögű, és így teljesül rá Pitagorasz tétele, \(\displaystyle QC^2 + PQ^2=PC^2\). De a korábbiak alapján \(\displaystyle PQ=PB\) és \(\displaystyle QC=P'A'=PA\), ezeket a fenti Pitagorasz-egyenlőségbe helyettesítve pedig pont \(\displaystyle PA^2+ PB^2 = PC^2\) adódik. Ezzel az állítást igazoltuk.

2. megoldás. Használjuk az alábbi ábrát és jelöléseit!

Az általánosság megszorítása nélkül legyen az \(\displaystyle ABC\) háromszög oldala egységnyi hosszú. Tükrözzük a \(\displaystyle C\) és a \(\displaystyle P\) pontokat az \(\displaystyle AB\) szakasz \(\displaystyle F\) felezőpontjára. Ekkor a \(\displaystyle C\) pont \(\displaystyle C'\) képe az \(\displaystyle APB\) köréírt körének a középpontja, hiszen \(\displaystyle APB \sphericalangle = 150^{\circ}\) miatt \(\displaystyle APB\) körén a rövidebb \(\displaystyle AB\) ívhez \(\displaystyle 30^{\circ}\)-os kerületi szög, és így \(\displaystyle 60^{\circ}\)-os középponti szög tartozik. De ekkor \(\displaystyle C'P=C'A=CA=1\), valamint \(\displaystyle CC'=2CF = 2 \cdot \sqrt{3}/2 = \sqrt{3}\) (az \(\displaystyle ABC\) szabályos háromszög magasságának a duplája).

Továbbá az \(\displaystyle APBP'\) és \(\displaystyle CPC'P'\) négyszögek paralelogrammák (hiszen középpontosan szimmetrikusak), így felírva külön-külön a paralellogrammatételt rájuk:

\(\displaystyle 2 AP^2 + 2 BP^2 = AB^2+PP'^2\), majd \(\displaystyle 2 AP^2 + 2 BP^2 = 1+PP'^2\), illetve \(\displaystyle 2 CP^2 + 2 C'P^2 = CC'^2 + PP'^2\), innen \(\displaystyle 2 CP^2 + 2 = 3 + PP'^2\) és így \(\displaystyle 2 CP^2=1 + PP'^2\) adódik. Mivel mind \(\displaystyle 2 CP^2\), mind a \(\displaystyle 2 AP^2 + 2 BP^2\) összeg is \(\displaystyle 1 + PP'^2\)-tel egyenlő, ezért egymással is egyenlőek, azaz (2-vel osztva) \(\displaystyle AP^2 + BP^2 = CP^2\). Ezzel az állítást igazoltuk.

Statistics:

102 students sent a solution.
4 points:	66 students.
3 points:	14 students.
2 points:	8 students.
1 point:	2 students.
0 point:	2 students.
Not shown because of missing birth date or parental permission:	6 solutions.

Problems in Mathematics of KöMaL, February 2024