Problem B. 5371. (February 2024)

B. 5371. Let point \(\displaystyle P\) be chosen inside triangle \(\displaystyle ABC\). Let \(\displaystyle D\), \(\displaystyle E\) and \(\displaystyle F\) denote the orthogonal projections of point \(\displaystyle P\) onto sides \(\displaystyle BC\), \(\displaystyle CA\) and \(\displaystyle AB\), respectively. Prove that \(\displaystyle \frac{PE+PF}{PA}+\frac{PF+PD}{PB}+\frac{PD+PE}{PC}\le 3\).

Proposed by Mihály Bencze, Brasov

(5 pont)

Deadline expired on March 11, 2024.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Legyenek a háromszög szögei \(\displaystyle \alpha\), \(\displaystyle \beta\), \(\displaystyle \gamma\), továbbá \(\displaystyle EAP\sphericalangle=\alpha_1\), \(\displaystyle PAF\sphericalangle=\alpha_2\), \(\displaystyle FBP\sphericalangle=\beta_1\), \(\displaystyle PBD\sphericalangle=\beta_2\) és \(\displaystyle DCP\sphericalangle=\gamma_1\), \(\displaystyle PCE\sphericalangle=\gamma_2\).

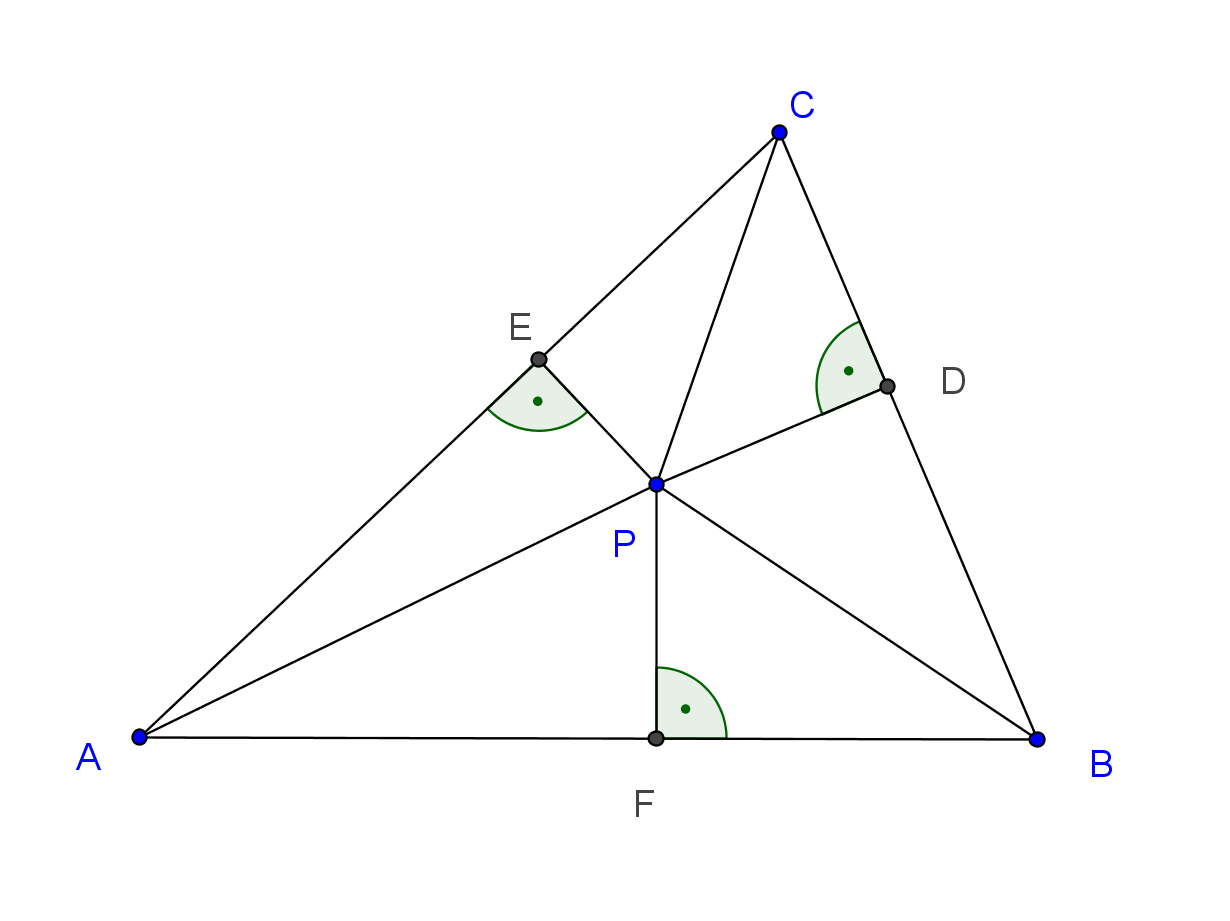
A \(\displaystyle PEA\) és \(\displaystyle PFA\) derékszögű háromszögekből a \(\displaystyle PE\) és \(\displaystyle PF\) szakaszok hosszát a \(\displaystyle PA\) szakasszal és szinusz szögfüggvénnyel is kifejezhetjük.

\(\displaystyle PE+PF=PA(\sin \alpha_1 +\sin \alpha_2). \)

A szinuszok összegére vonatkozó addíciós tétel alapján, továbbá felhasználva, hogy a koszinusz szögfüggvény értéke legfeljebb \(\displaystyle 1\), kapjuk a következő becslést:

\(\displaystyle \frac{PE+PF}{PA}=\sin \alpha_1 +\sin \alpha_2=2\sin \frac{\alpha_1+\alpha_2}{2}\cos\frac{\alpha_1-\alpha_2}{2}\le 2\sin\frac{\alpha}{2}.\)

Egyenlőség csak \(\displaystyle \alpha_1=\alpha_2\) esetén. Ugyanezzel a módszerrel kapjuk, hogy

\(\displaystyle \frac{PF+PD}{PB}\le 2\sin \frac{\beta}{2} \quad \text{és} \quad \frac{PD+PE}{PC}\le 2\sin\frac{\gamma}{2}.\)

Alkalmazzuk végül a szinuszfüggvényre és az \(\displaystyle \frac{\alpha}{2}, \frac{\beta}{2}, \frac{\gamma}{2}\) hegyesszögekre a Jensen-egyenlőtlenséget. A szinuszfüggvény a \(\displaystyle \left[0, \frac{\pi}{2} \right]\) intervallumon konkáv, ezért

\(\displaystyle \frac{PE+PF}{PA}+\frac{PF+PD}{PB}+\frac{PD+PE}{PC}\le 2\left(\sin\frac{\alpha}{2}+\sin\frac{\beta}{2}+\sin\frac{\gamma}{2}\right) \le 2\cdot 3\cdot \sin \frac{\alpha+\beta+\gamma}{6}=3.\)

Összességében egyenlőség az első becslésnél a szögfelezők esetében, míg a második becslésnél a szinuszfüggvény szigorú konkávitása miatt csak szabályos háromszög esetén teljesül. Tehát egyenlőség csak abban az esetben igaz, ha a \(\displaystyle P\) pont egy \(\displaystyle ABC\) szabályos háromszög középpontja.

Statistics:

61 students sent a solution.
5 points:	Ali Richárd, Aravin Peter, Baráth Borbála, Bencze Mátyás, Bodor Mátyás, Bui Thuy-Trang Nikolett, Christ Miranda Anna, Csonka Illés, Csupor Albert Dezső, Danka Emma, Diaconescu Tashi, Erdélyi Kata, Farkas 005 Bendegúz, Farkas Ábel, Forrai Boldizsár, Gábor Benjámin, Görömbey Tamás, Holló Martin, Horák Zsófia, Jármai Roland, Juhász-Molnár Erik, Kerekes András, Keresztély Zsófia, Klement Tamás, Kovács Benedek Noel, Körmöndi Márk, Kővágó Edit Gréta, Molnár István Ádám, Morvai Várkony Albert, Op Den Kelder Ábel, Petrányi Lilla, Pletikoszity Martin, Prohászka Bulcsú, Puppi Barna, Romaniuc Albert-Iulian, Sági Mihály, Sánta Gergely Péter, Sárdinecz Dóra, Sha Jingyuan, Szakács Ábel, Török Eszter Júlia, Varga 511 Vivien, Vigh 279 Zalán, Virág Lénárd Dániel, Virág Tóbiás, Wágner Márton, Zhai Yu Fan.
4 points:	4 students.
3 points:	4 students.
2 points:	3 students.
0 point:	1 student.
Not shown because of missing birth date or parental permission:	1 solutions.

Problems in Mathematics of KöMaL, February 2024