Problem B. 5377. (March 2024)

B. 5377. Determine the set of real numbers \(\displaystyle p\) satisfying the following property: inequality \(\displaystyle \sqrt{a^2+b^2-ab}+\sqrt{b^2+c^2-bc}\geq \sqrt{a^2+c^2-p\cdot ac}\) holds for all triples of positive real numbers \(\displaystyle a\), \(\displaystyle b\) and \(\displaystyle c\), for which the square roots are defined.

Proposed by Zoltán Lóránt Nagy, Budapest

(4 pont)

Deadline expired on April 10, 2024.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Vegyük észre, hogy a kifejezés a koszinusztételre emlékeztet: \(\displaystyle x^2+y^2-2xy\cos(60^{\circ})=z^2\) teljesül egy \(\displaystyle x\), \(\displaystyle y\), \(\displaystyle z\) oldalú háromszögben, ahol \(\displaystyle z\)-vel szemben \(\displaystyle 60^{\circ}\) van.

Ez motivál arra, hogy felvegyük az \(\displaystyle O\), \(\displaystyle A\), \(\displaystyle B\), \(\displaystyle C\) pontokat a síkon úgy, hogy

\(\displaystyle OA = a, OB = b \text{ és } OC = c, \)

illetve

\(\displaystyle AOB \sphericalangle = BOC \sphericalangle = 60^{\circ} \text{ és } AOC \sphericalangle = 120^{\circ}. \)

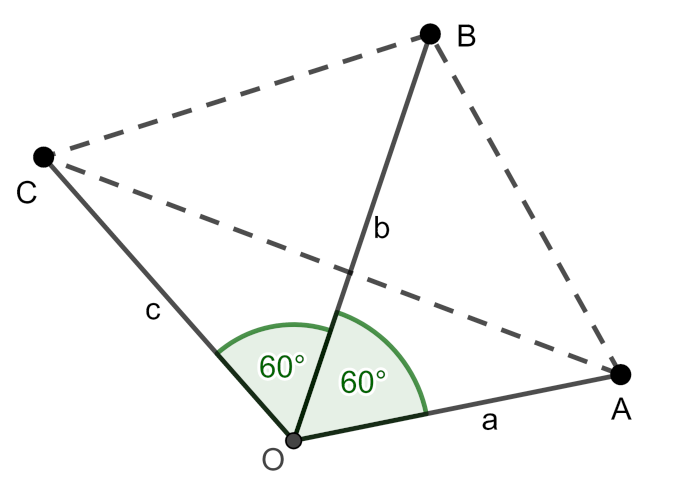
Ekkor a koszinusztétel szerint

\(\displaystyle AB = \sqrt{a^2+b^2-ab}, \quad BC = \sqrt{b^2+c^2-bc}, \quad AC = \sqrt{a^2+c^2+ac}. \)

A háromszög-egyenlőtlenség szerint \(\displaystyle AB + BC \geq AC \), ebből \(\displaystyle p \geq -1\) esetén

\(\displaystyle \sqrt{a^2+b^2-ab} + \sqrt{b^2+c^2-bc} \geq \sqrt{a^2+c^2+ac} \geq \sqrt{a^2+c^2-p \cdot ac}. \)

\(\displaystyle p < -1\) esetén ugyanakkor lehet olyan \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\) számhármast találni, amelyre nem teljesül az egyenlőtlenség. Válasszuk az \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\) számokat úgy, hogy az \(\displaystyle A\), \(\displaystyle B\), \(\displaystyle C\) pontok egy egyenesre essenek, például \(\displaystyle a=2\), \(\displaystyle b=1\), \(\displaystyle c=2\). Ekkor

\(\displaystyle \sqrt{2^2+1^2-2 \cdot 1} + \sqrt{1^2+2^2-1 \cdot 2} = \sqrt{3} + \sqrt{3} = \sqrt{12} = \sqrt{2^2+2^2+2 \cdot 2} < \sqrt{2^2+2^2-p \cdot 2 \cdot 2}. \)

Tehát a keresett \(\displaystyle p\) értékek halmaza a \(\displaystyle [-1,\infty)\) intervallum.

Statistics:

50 students sent a solution.
4 points:	Ali Richárd, Aravin Peter, Baráth Borbála, Bencze Mátyás, Bodor Mátyás, Bui Thuy-Trang Nikolett, Csató Hanna Zita , Csupor Albert Dezső, Diaconescu Tashi, Erdélyi Kata, Farkas 005 Bendegúz, Fekete Aron, Fórizs Emma, Forrai Boldizsár, Görömbey Tamás, Holló Martin, Kerekes András, Kovács Benedek Noel, Németh Bernát, Pletikoszity Martin, Prohászka Bulcsú, Szabó 721 Sámuel, Veres Dorottya, Virág Lénárd Dániel, Wágner Márton.
3 points:	Christ Miranda Anna, Horák Zsófia, Keresztély Zsófia, Klement Tamás, Kővágó Edit Gréta, Nagypál Katóca, Petrányi Lilla, Sárdinecz Dóra, Szabó Imre Bence, Vigh 279 Zalán.
2 points:	5 students.
1 point:	3 students.
0 point:	6 students.
Not shown because of missing birth date or parental permission:	1 solutions.

Problems in Mathematics of KöMaL, March 2024