 Problem B. 5379. (March 2024)
Problem B. 5379. (March 2024)
B. 5379. Let \(\displaystyle ABC\) be a triangle with a right angle at \(\displaystyle C\). On the hypotenuse \(\displaystyle AB\), let \(\displaystyle H\) and \(\displaystyle D\) be the feet of the altitude and the angle bisector starting from \(\displaystyle C\), respectively. The bisector of angle \(\displaystyle AHC\) meets \(\displaystyle AC\) at point \(\displaystyle E\), and the bisector of angle \(\displaystyle CHB\) meets \(\displaystyle BC\) at \(\displaystyle F\). Mark a point \(\displaystyle M\) on line segment \(\displaystyle HE\) and a point \(\displaystyle N\) on line segment \(\displaystyle HF\) that satisfy \(\displaystyle HM:HE=HN:HF\). Show that lines \(\displaystyle CD\), \(\displaystyle AM\) and \(\displaystyle BN\) are concurrent.
Proposed by Nguyen Duy Khanh, Vietnam
(5 pont)
Deadline expired on April 10, 2024.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Legyen \(\displaystyle P=AM\cap BN\), és jelölje \(\displaystyle d(X,YZ)\) az \(\displaystyle X\) pont és az \(\displaystyle YZ\) egyenes (előjeles) távolságát; azt kell igazolni, hogy \(\displaystyle P\) rajta van az \(\displaystyle ACB\) szögfelezőjén, vagyis \(\displaystyle d(P,BC)=d(P,CA)\).
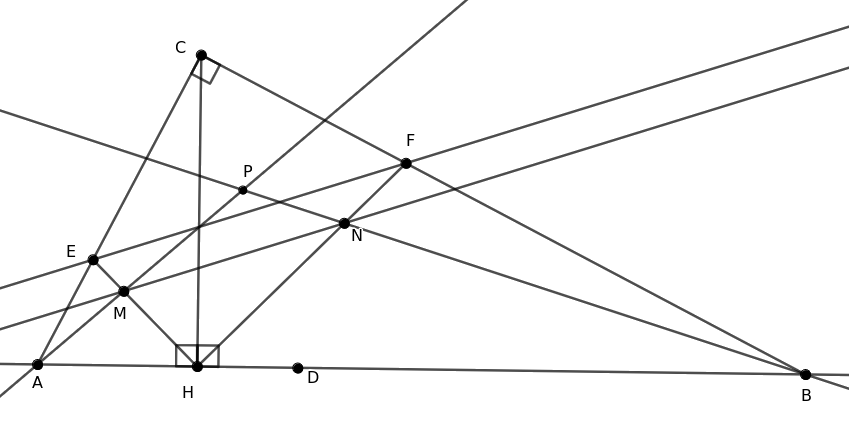
Legyen \(\displaystyle x=\dfrac{ME}{HE}=\dfrac{HN}{HF}\), ekkor
$$\begin{gather*} \dfrac{d(P,AC)}{d(P,AB)} = \dfrac{d(M,AC)}{d(M,AB)} = \dfrac{d(M,AC)}{d(M,HC)} = \dfrac{x\cdot d(H,AC)}{(1-x)\cdot d(E,HC)} = \dfrac{x}{1-x}\cdot\dfrac{d(H,AC)}{d(E,HC)}. \end{gather*}$$Az első egyenlőségnél azt használtuk ki, hogy az \(\displaystyle A\), \(\displaystyle M\) és \(\displaystyle P\) pontok kollineárisak; a másodiknál, hogy \(\displaystyle MH\) felezi a \(\displaystyle CHA\) szöget; a harmadiknál pedig a párhuzamos szelőszakaszok tételét alkalmaztuk kétszer. Hasonlóan, de a második lépést kihagyva láthatjuk be, hogy
\(\displaystyle \dfrac{d(P,BC)}{d(P,AB)}=\dfrac{d(N,BC)}{d(N,AB)}=\dfrac{x\cdot d(H,BC)}{(1-x)\cdot d(F,AB)}=\dfrac{x}{1-x}\cdot\dfrac{d(H,BC)}{d(F,AB)}.\)
Végül vegyük észre, hogy az a \(\displaystyle H\) körüli forgatva nyújtás, ami a \(\displaystyle BCH\) háromszöget a \(\displaystyle CAH\) háromszögbe viszi, egyúttal \(\displaystyle E\)-t \(\displaystyle F\)-be viszi. Mivel a hasonlóság megtartja a megfelelő szakaszok arányát, így
\(\displaystyle \dfrac{d(H,AC)}{d(E,HC)}=\dfrac{d(H,BC)}{d(F,AB)}.\)
Az eddigiek összevetéséből
\(\displaystyle \dfrac{d(P,AC)}{d(P,AB)}=\dfrac{d(P,BC)}{d(P,AB)}\)
adódik, tehát valóban \(\displaystyle d(P,AC)=d(P,BC)\). Ezzel a bizonyítást befejeztük.
Statistics:
42 students sent a solution. 5 points: Ali Richárd, Bencze Mátyás, Bodor Mátyás, Bogdán Balázs Ákos, Bui Thuy-Trang Nikolett, Csonka Illés, Csupor Albert Dezső, Diaconescu Tashi, Erdélyi Kata, Farkas 005 Bendegúz, Fórizs Emma, Gyenes Károly, Hodossy Réka, Holló Martin, Horák Zsófia, Jármai Roland, Klement Tamás, Kovács Benedek Noel, Miklós Janka, Petrányi Lilla, Prohászka Bulcsú, Puppi Barna, Romaniuc Albert-Iulian, Sági Mihály, Sárdinecz Dóra, Sha Jingyuan, Sütő Áron, Szabó 721 Sámuel, Veres Dorottya, Vigh 279 Zalán, Virág Tóbiás, Zhai Yu Fan. 4 points: Baráth Borbála, Forrai Boldizsár, Kerekes András, Virág Lénárd Dániel. 3 points: 1 student. 2 points: 2 students. 1 point: 2 students. 0 point: 1 student.
Problems in Mathematics of KöMaL, March 2024
