Problem B. 5381. (March 2024)

B. 5381. Let \(\displaystyle ABCDEFGH\) be a cyclic octagon inscribed in circle \(\displaystyle \Omega_1\) and let \(\displaystyle \Omega_2\) be another circle inside \(\displaystyle \Omega_1\). Assume that circles \(\displaystyle \omega_1\), \(\displaystyle \omega_2\), \(\displaystyle \omega_3\), \(\displaystyle \omega_4\) are tangent to \(\displaystyle \Omega_2\) externally; moreover, \(\displaystyle \omega_1\) is tangent to arc \(\displaystyle AB\) of \(\displaystyle \Omega_1\) internally, and tangent to line segments \(\displaystyle AF\) and \(\displaystyle BE\); \(\displaystyle \omega_2\) is tangent to arc \(\displaystyle CD\) internally, and tangent to \(\displaystyle CH\) and \(\displaystyle DG\); \(\displaystyle \omega_3\) is tangent to arc \(\displaystyle EF\) internally, and tangent to \(\displaystyle AF\) and \(\displaystyle BE\); finally, \(\displaystyle \omega_4\) is tangent to arc \(\displaystyle GH\) internally, and tangent to \(\displaystyle CH\) and \(\displaystyle DG\), as shown in the figure. Prove that the quadrilateral enclosed by segments \(\displaystyle AF\), \(\displaystyle BE\), \(\displaystyle CH\) and \(\displaystyle DG\) has an inscribed circle.

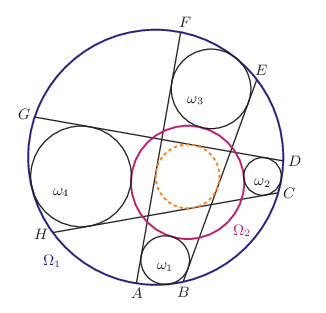
Proposed by Géza Kós, Budapest

(6 pont)

Deadline expired on April 10, 2024.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Térbe kilépéssel, a körökre illesztett kúpokkal bizonyítunk.

Az \(\displaystyle AF\) egyenesnek a \(\displaystyle B\), \(\displaystyle E\) pontokat tartalmazó oldalát az egyenes belső oldalának fogjuk hívni, és ugyanígy, a \(\displaystyle BE\), \(\displaystyle CH\) és \(\displaystyle DG\) egyeneseknek az \(\displaystyle A\), \(\displaystyle F\), a \(\displaystyle D\), \(\displaystyle G\), illetve \(\displaystyle C\), \(\displaystyle H\) pontokat tartalmazó oldalát is az illető egyenes belső oldalának nevezzük. A feladatunk egy olyan kör megszerkesztése, amely az \(\displaystyle AF\), a \(\displaystyle BE\), a \(\displaystyle CH\) és a \(\displaystyle DG\) egyenest is a belső oldalán érinti.

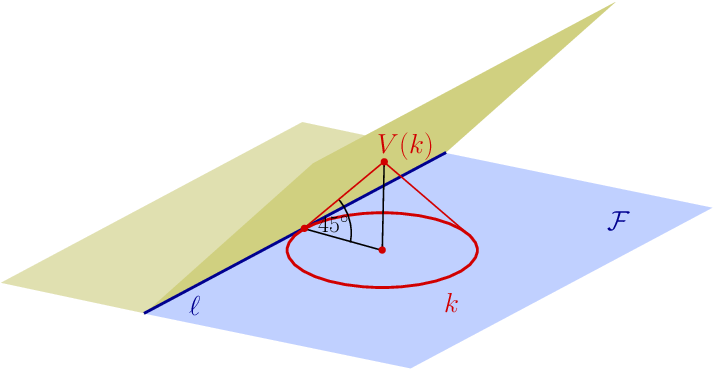
Az ábra síkját – a továbbiakban alapksíknak fogjuk hívni – helyezzük el a térben. A sík egyik oldalára mondjuk azt, hogy a sík fölött van. Például, az alapsík lehet a térbeli derékszögű koordináta-rendszer \(\displaystyle x\)–\(\displaystyle y\) síkja, az alapsík fölötti pontok a pozitív \(\displaystyle z\)-koordinátájú pontok. Az alapsíkban fekvő köröket feleltessük meg az alapsík fölötti féltér pontjainak a következőképpen. Ha \(\displaystyle k\) tetszőleges kör a síkban, akkor illesszünk rá egy \(\displaystyle 45^\circ\)-os meredekségű kúpot; a kúp csúcsát jelöljük \(\displaystyle V(k)\)-val. Másképpen fogalmazva, ha \(\displaystyle k\) az \(\displaystyle (x,y)\) középpontú, \(\displaystyle r\) sugarú kör, akkor legyen \(\displaystyle V(k)=(x,y,r)\). Megfordítva, minden, a sík fölötti \(\displaystyle P=(x,y,r)\) ponthoz létezik egy \(\displaystyle 45^\circ\)-os meredekségű kúp, amelynek csúcsa \(\displaystyle V\), és alapköre az alapsíkban van, nevezetesen az \(\displaystyle (x,y)\) középpontú, \(\displaystyle r\) sugarú kör; jelöljük ezt a kört \(\displaystyle \kappa(P)\)-vel.

Szükségünk lesz a következő egyszerű észrevételre. Tegyük fel, hogy az alapsíkban adott egy \(\displaystyle \ell\) határú \(\displaystyle \mathcal{F}\) félsík, és vizsgáljuk azokat a \(\displaystyle k\) köröket, amelyek \(\displaystyle \mathcal{F}\)-ben fekszenek, és érintik \(\displaystyle \ell\)-et. Látható, hogy az összes ilyen körökhöz tartozó \(\displaystyle V(k)\) pontok halmaza egy félsík, ami illeszkedik \(\displaystyle \ell\)-re, az \(\displaystyle \mathcal{F}\)-fel \(\displaystyle 45^\circ\)-os szöget zár be, és persze az alapsík felső oldalán van.

Tekintsük az alapsíkban azokat a \(\displaystyle k\) köröket, amelyek az \(\displaystyle AF\) egyenest a belső oldalán érintik. A fenti észrevétel szerint a \(\displaystyle V(k)\) pontok egy \(\displaystyle AF\)-re illeszkedő \(\displaystyle \mathcal{F}_{AF}\) félsíkban vannak. Hasonlóan, a \(\displaystyle BE\), \(\displaystyle CH\) és \(\displaystyle DG\) egyeneseket a belső oldalukon érintő körökhöz rendelt csúcsok is egy-egy, az illető egyenesre illesztett félsík, \(\displaystyle \mathcal{F}_{BE}\), \(\displaystyle \mathcal{F}_{CH}\), illetve \(\displaystyle \mathcal{F}_{DG}\) pontjai. A feladat megoldásához azt kell igazolnunk, hogy az \(\displaystyle \mathcal{F}_{AF}\), \(\displaystyle \mathcal{F}_{BE}\), \(\displaystyle \mathcal{F}_{CH}\), \(\displaystyle \mathcal{F}_{DG}\) félsíkoknak van egy közös \(\displaystyle W\) pontja.

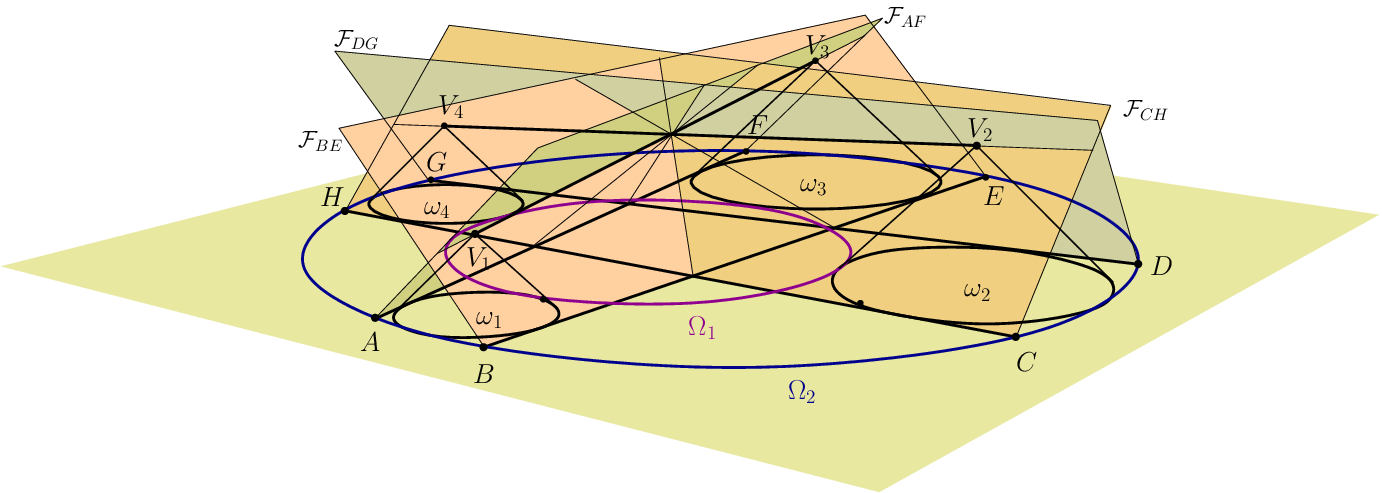
Legyen \(\displaystyle V_1=V(\omega_1)\), \(\displaystyle V_2=V(\omega_2)\), \(\displaystyle V_3=V(\omega_3)\), illetve \(\displaystyle V_4=V(\omega_4)\). Mivel \(\displaystyle \omega_1\) és \(\displaystyle \omega_3\) a belső oldalon érinti az \(\displaystyle AF\) és a \(\displaystyle BE\) egyenest, az \(\displaystyle \mathcal{F}_{AF}\) és \(\displaystyle \mathcal{F}_{BE}\) félsíkoknak \(\displaystyle V_1\) és \(\displaystyle V_3\) is közös pontja, ezért mindkét félsík tartalmazza a \(\displaystyle V_1V_3\) szakaszt. Hasonlóan, az \(\displaystyle \mathcal{F}_{CH}\) és a \(\displaystyle \mathcal{F}_{DG}\) félsík is tartalmazza a \(\displaystyle V_2V_4\) szakaszt.

Most megmutatjuk, hogy a \(\displaystyle V_1V_3\) és \(\displaystyle V_2V_4\) szakaszok egy síkban fekszenek. Illesszük az \(\displaystyle \Omega_1\) körre a \(\displaystyle \mathcal{G}_1\), az \(\displaystyle \Omega_2\)-re a \(\displaystyle \mathcal{G}_2\) gömböt úgy, hogy ezek \(\displaystyle 45^\circ\)-os szögben messék az alapsíkot, \(\displaystyle \mathcal{G}_1\) középpontja az alapsík fölött, \(\displaystyle \mathcal{G}_2\) középpontja a sík alatt legyen. Legyen \(\displaystyle \omega_i\) és \(\displaystyle \Omega_1\) érintési pontja \(\displaystyle T_i\), az \(\displaystyle \omega_i\) és \(\displaystyle \Omega_2\) érintési pontja pedig \(\displaystyle U_i\). Az \(\displaystyle \omega_i\)-re emelt kúp \(\displaystyle V_iT_i\) alkotója érinti \(\displaystyle \mathcal{G}_1\)-et, míg ugyanennek a kúpnak a \(\displaystyle V_iU_i\) alkotója érinti \(\displaystyle \mathcal{G}_2\)-t. A \(\displaystyle V_i\) csúcsból tehát ugyanolyan hosszú érintőt lehet húzni a két gömbhöz, tehát mindegyik \(\displaystyle V_i\) csúcs a két gömb hatványsíkjában van.

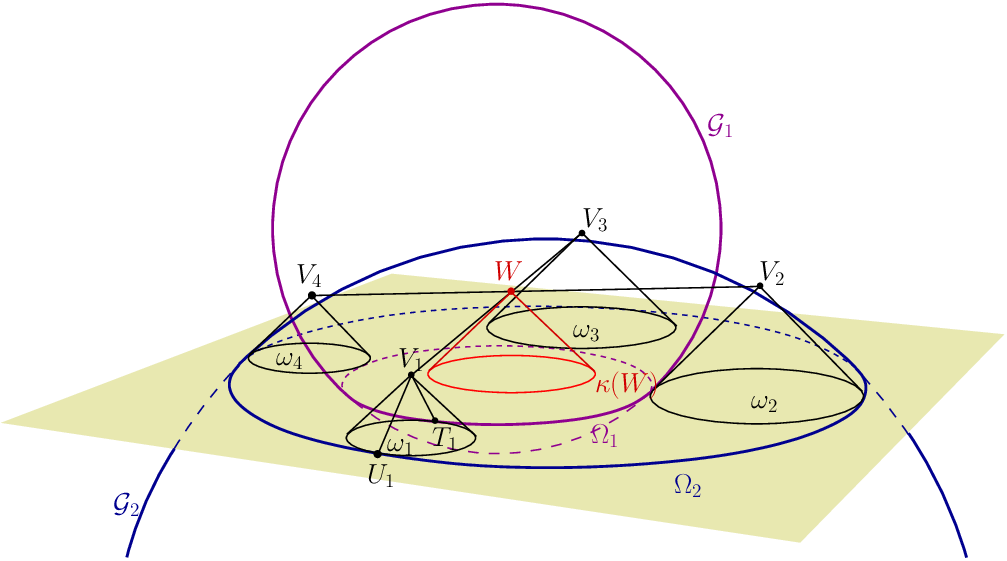
A \(\displaystyle V_1V_3\) és \(\displaystyle V_2V_4\) szakaszok merőleges vetülete az ábra síkjára az \(\displaystyle AF\) és a \(\displaystyle BE\), illetve a \(\displaystyle CH\) és \(\displaystyle DG\) egyenesek középvonalai, ezek metszik az \(\displaystyle AF\), \(\displaystyle BE\), \(\displaystyle CH\) és \(\displaystyle DG\) egyenesek által meghatározott négyszög odalait, és a négyszög belsejében metszik egymást. Ezért az (egy síkban fekvő) \(\displaystyle V_1V_3\) és \(\displaystyle V_2V_4\) szakaszok is metszik egymást a térben. Legyen \(\displaystyle W\) a két szakasz metszéspontja; ekkor tehát \(\displaystyle W\) közös pontja az \(\displaystyle \mathcal{F}_{AF}\), \(\displaystyle \mathcal{F}_{BE}\), \(\displaystyle \mathcal{F}_{CH}\), \(\displaystyle \mathcal{F}_{DG}\) félsíkoknak, vagyis a \(\displaystyle \kappa(W)\) kör a belső oldalán érinti az \(\displaystyle AF\), \(\displaystyle BE\), \(\displaystyle CH\), \(\displaystyle DG\) egyeneseket.

Statistics:

3 students sent a solution.
6 points:	Bodor Mátyás, Forrai Boldizsár, Virág Tóbiás.

Problems in Mathematics of KöMaL, March 2024