Problem B. 5398. (September 2024)

B. 5398. In trapezoid \(\displaystyle ABCD\) the bases are \(\displaystyle AB \parallel CD\) and \(\displaystyle \angle ADC - \angle CBA = 90^{\circ}\). Prove that the sum of the squares of the legs equals the difference of the squares of the bases.

Proposed by Miklós Oláh, Szilágykraszna

(3 pont)

Deadline expired on October 10, 2024.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. A trapéz oldalainak hosszúsága legyen \(\displaystyle AB=a\), \(\displaystyle BC=b\), \(\displaystyle CD=c\), \(\displaystyle DA=d\). A \(\displaystyle D\) ponton átmenő, \(\displaystyle BC\)-vel párhuzamos egyenesnek az \(\displaystyle AB\) alappal közös pontját jelölje \(\displaystyle E\).

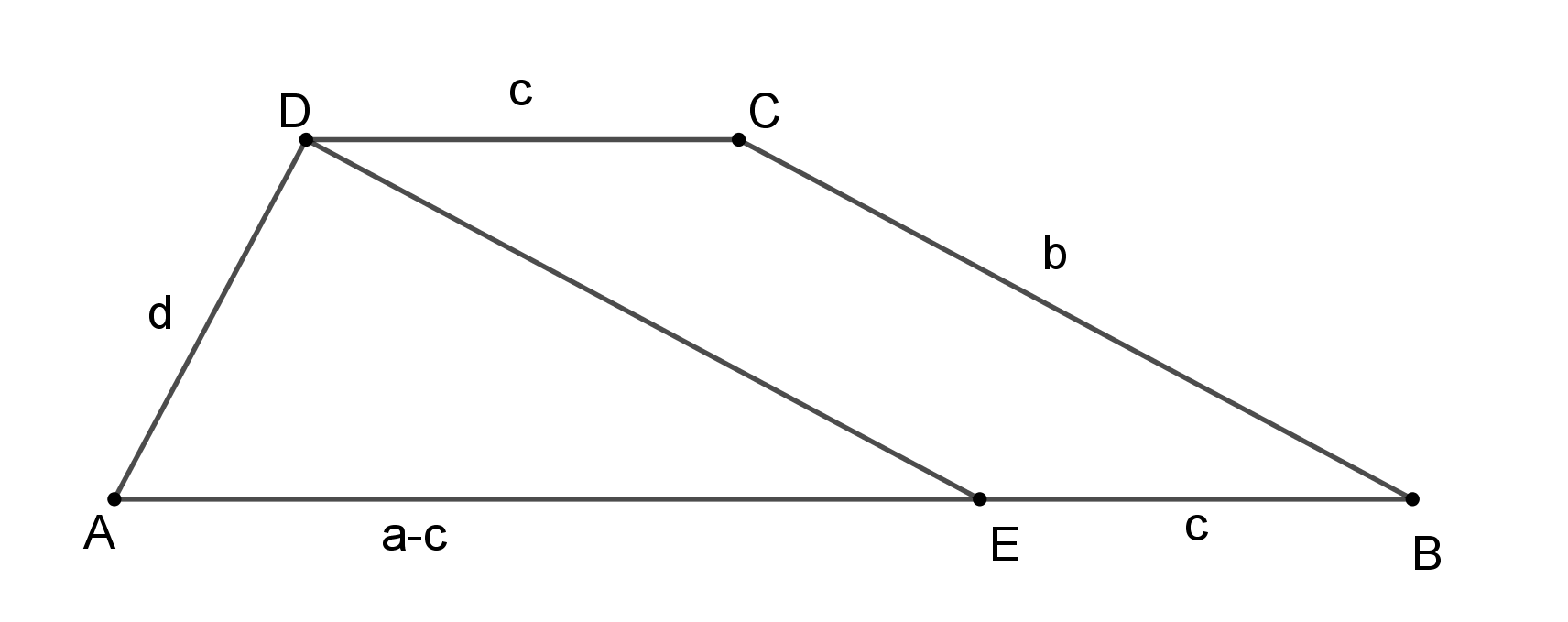
Az \(\displaystyle EBCD\) négyszög szemköztes oldalai párhuzamosak lévén \(\displaystyle EBCD\) paralelogramma, ezért \(\displaystyle EB=c\), így \(\displaystyle AE=a-c\), továbbá \(\displaystyle ED=b\) és \(\displaystyle EDC\sphericalangle=CBA\sphericalangle\). Ezért \(\displaystyle ADE\sphericalangle = ADC\sphericalangle - EDC\sphericalangle = ADC\sphericalangle - CBA\sphericalangle = 90^{\circ}\). Az \(\displaystyle AD=d\), \(\displaystyle ED=b\) befogójú, \(\displaystyle AE=a-c\) átfogójú derékszögű háromszögben Pitagorasz tétele szerint \(\displaystyle d^2+b^2=(a-c)^2\).

Statistics:

176 students sent a solution.
3 points:	115 students.
2 points:	24 students.
1 point:	16 students.
0 point:	3 students.
Not shown because of missing birth date or parental permission:	10 solutions.

Problems in Mathematics of KöMaL, September 2024