Problem B. 5408. (October 2024)

B. 5408. In a triangle the length of one of the sides is the arithmetic mean of the lengths of the other two sides. Prove that the length of the angle bisector corresponding to the middle side is \(\displaystyle \frac{\sqrt{3}}{2}\) times the geometric mean of the lengths of the other two sides.

Proposed by Mihály Hujter, Budapest

(4 pont)

Deadline expired on November 11, 2024.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Az \(\displaystyle ABC\) háromszög oldalait jelölje \(\displaystyle BC=a\), \(\displaystyle AC=b\), \(\displaystyle AB=(a+b)/2\); a \(\displaystyle C\)-ből induló belső szögfelező \(\displaystyle CD=f\), \(\displaystyle BD=k\), \(\displaystyle AD=l\) az ábra szerint. A feladat feltétele: \(\displaystyle k+l= \dfrac{a+b}{2}\).

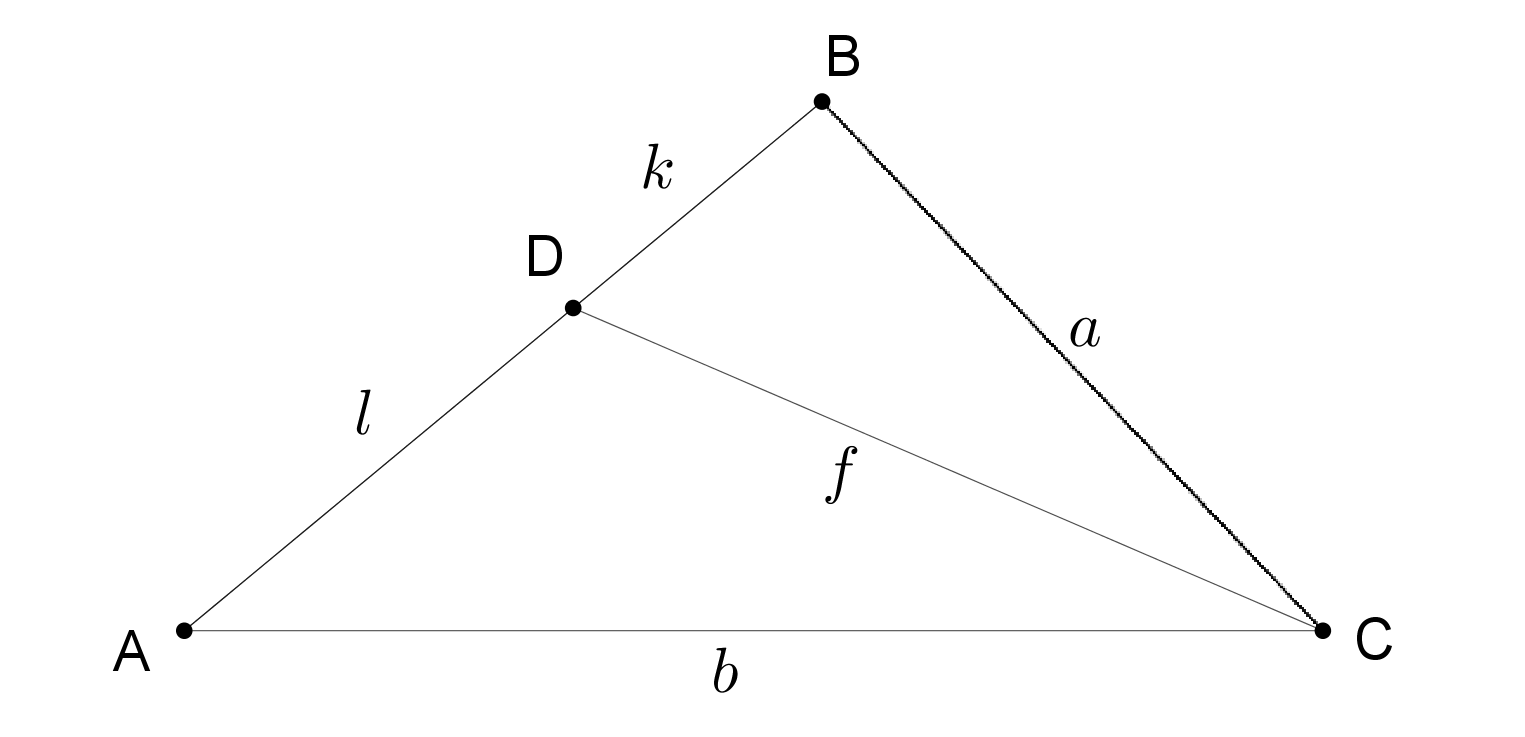
A belső szögfelezővel kapcsolatos ismert összefüggések: \(\displaystyle \dfrac{k}{l} = \dfrac{a}{b}\) és \(\displaystyle f^2 = ab - kl\). Az első összefüggésből \(\displaystyle k=\dfrac{a}{b}\cdot l\), így

\(\displaystyle \dfrac{a+b}{2} = k+l = \dfrac{a}{b}\cdot l + l = \dfrac{a+b}{b}\cdot l, \)

amiből \(\displaystyle l = \dfrac{b}{2}\), ezért \(\displaystyle k = k+l - l = \dfrac{a+b}{2} - \dfrac{b}{2} = \dfrac{a}{2}\). Tehát valóban

\(\displaystyle f^2 = ab - kl = ab - \dfrac{a}{2}\cdot \dfrac{b}{2} = \dfrac{3}{4}ab, \)

azaz \(\displaystyle f = \dfrac{\sqrt{3}}{2}\cdot \sqrt{ab}\).

Statistics:

119 students sent a solution.
4 points:	55 students.
3 points:	39 students.
2 points:	5 students.
1 point:	5 students.
0 point:	6 students.
Not shown because of missing birth date or parental permission:	3 solutions.

Problems in Mathematics of KöMaL, October 2024