Problem B. 5413. (October 2024)

B. 5413. Let \(\displaystyle M\) be the orthocenter, \(\displaystyle S\) be the centroid and \(\displaystyle I\) be the incenter of the non-equilateral triangle \(\displaystyle ABC\). Prove that \(\displaystyle \angle MIS>90^\circ\).

Proposed by Viktor Vígh, Sándorfalva

(6 pont)

Deadline expired on November 11, 2024.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Használjuk a szokásos jelöléseket, a körülírt kör középpontja legyen \(\displaystyle O\). A koszinusztétel miatt elegendő lenne megmutatni, hogy \(\displaystyle MS^2-IS^2-IM^2>0.\)

Ehhez először is elevenítsük fel, hogy az \(\displaystyle M\), \(\displaystyle S\) és \(\displaystyle O\) pontok a háromszög Euler-egyenesén helyezkednek el, \(\displaystyle S\) az \(\displaystyle MO\) szakasz \(\displaystyle O\)-hoz közelebbi harmadolópontja. Írjuk fel az \(\displaystyle MOI\) háromszögben a Stewart-tételt az \(\displaystyle IS\) szakaszra:

\(\displaystyle IM^2\cdot SO+IO^2\cdot MS=MO\cdot IS^2+MO\cdot MS\cdot SO.\)

Felhasználva, hogy \(\displaystyle S\) harmadol, osszuk mindkét oldalt \(\displaystyle SO\)-val, s így nyerjük, hogy

\(\displaystyle IM^2+2IO^2=3IS^2+MO\cdot MS=3IS^2+\frac 32 MS^2.\)

Ebből rendezéssel adódik, hogy

\(\displaystyle IS^2=\frac 23 IO^2+ \frac 13 IM^2-\frac 12 MS^2.\)

Ezt behelyettesítve \(\displaystyle IS^2\) helyére:

\(\displaystyle MS^2-IS^2-IM^2=MS^2-\frac 23 IO^2- \frac 13 IM^2+\frac 12 MS^2-IM^2=\frac 32 MS^2-\frac 23 IO^2-\frac 43 IM^2=\frac 23\left (MO^2- IO^2-2 IM^2 \right ).\)

A továbbiakban a zárójelben lévő kifejezésről igazoljuk, hogy pozitív. Először is az Euler-tétel szerint \(\displaystyle IO^2=R^2-2Rr\), ahol \(\displaystyle R\) és \(\displaystyle r\) rendre a körülírható- és a beírható körök sugarai.

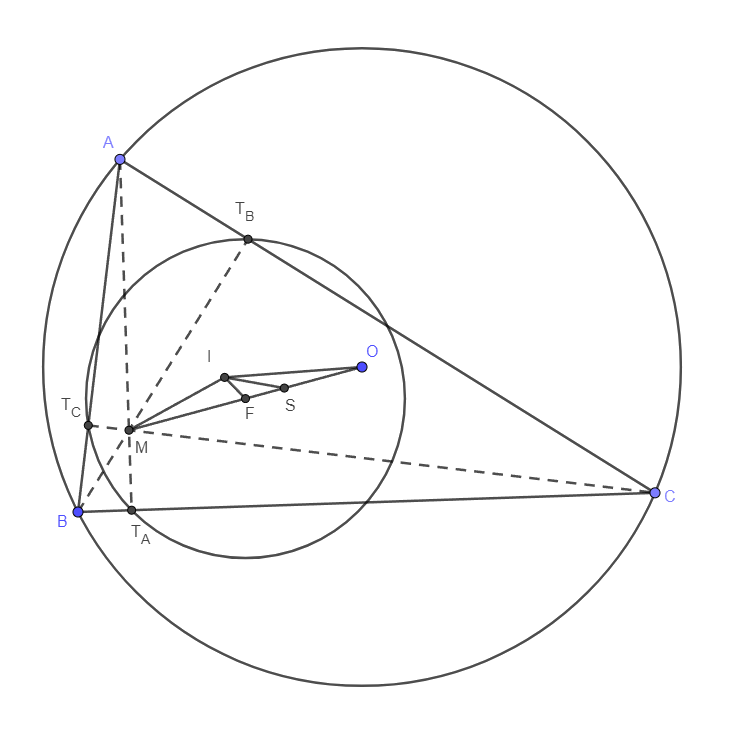
Tekintsük az \(\displaystyle ABC\) háromszög Feuerbach-körét, ennek sugara \(\displaystyle R/2\), középpontja pedig az \(\displaystyle MO\) szakasz \(\displaystyle F\) felezőpontja. A Feuerbach-tétel szerint ezen kört belülről érinti a beírt kör, ezért \(\displaystyle IF=R/2-r\).

Írjuk fel a (paralelogramma-tételből vagy a fentebb idézett Stewart-tételből következő) összefüggést az \(\displaystyle IMO\) háromszög \(\displaystyle IF\) súlyvonalára:

\(\displaystyle 2IM^2+2IO^2 = MO^2 + 4IF^2.\)

Ebből

\(\displaystyle MO^2-IO^2-2IM^2=IO^2-4IF^2=R^2-2Rr-4\left (\frac R2-r\right )^2=2Rr-4r^2=2r(R-2r).\)

A sugáregyenlőtlenség szerint \(\displaystyle R\ge 2r\) és egyenlőség csak szabályos háromszög esetén áll, így esetünkben \(\displaystyle MO^2-IO^2-2IM^2>0\), amivel a feladat állítását beláttuk.

Megjegyzés. Legyenek \(\displaystyle T_A\), \(\displaystyle T_B\) és \(\displaystyle T_C\) a megfelelő magasságok talppontjai. Jól ismert tény, hogy a \(\displaystyle T_AT_BT_C\) talpponti háromszög beírt körének középpontja éppen \(\displaystyle M\), ezen beírt kör sugarát jelölje \(\displaystyle \varrho\). A talpponti háromszög körülírt köre pedig éppen az \(\displaystyle ABC\) háromszög Feuerbach-köre. Így viszont ismét alkalmazhatjuk az Euler-tételt, ezúttal a talpponti háromszögre, és így kapjuk, hogy

\(\displaystyle OM^2=4MF^2=4\left [ \left (\frac R2\right )^2-2\cdot \frac R2 \cdot \varrho \right]=R^2-4R\varrho.\)

A megoldásban is használt \(\displaystyle 4IF^2=2IO^2+2IM^2-OM^2\) összefüggésből pedig \(\displaystyle IM^2=2r^2-2R\varrho\) adódik, így végül \(\displaystyle MO^2\), \(\displaystyle IO^2\) és \(\displaystyle IM^2\) mindegyikére elegáns formula adható \(\displaystyle R\), \(\displaystyle r\) és \(\displaystyle \varrho\) segítségével.

Statistics:

28 students sent a solution.
6 points:	Ali Richárd, Bencze Mátyás, Bui Thuy-Trang Nikolett, Diaconescu Tashi, Holló Martin, Kovács Benedek Noel, Prohászka Bulcsú, Sha Jingyuan, Virág Lénárd Dániel.
5 points:	Aravin Peter, Molnár Lili, Varga 511 Vivien, Zhai Yu Fan.
4 points:	4 students.
3 points:	2 students.
2 points:	3 students.
1 point:	1 student.
0 point:	4 students.

Problems in Mathematics of KöMaL, October 2024