Problem B. 5425. (December 2024)

B. 5425. Let \(\displaystyle ABCD\) be a cyclic quadrilateral, let \(\displaystyle E\) be the midpoint of \(\displaystyle AC\) and \(\displaystyle O\) be the centre of the circumcircle such that \(\displaystyle O\) and \(\displaystyle E\) are distinct. Prove that if \(\displaystyle OEBD\) is cyclic then \(\displaystyle EC\) bisects angle \(\displaystyle DEB\).

Proposed by: Ákos Somogyi, London

(4 pont)

Deadline expired on January 10, 2025.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Az \(\displaystyle ABCD\) körben \(\displaystyle OA=OB=OC=OD\) a kör sugarai.

Az \(\displaystyle OAC\) háromszög egyenlő szárú, ezért az \(\displaystyle OE\) egyenes a háromszög magassága: \(\displaystyle AC\perp OE\).

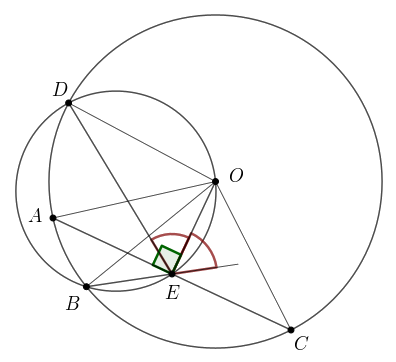
Az \(\displaystyle BEOD\) körben \(\displaystyle BO=DO\) miatt a \(\displaystyle BO\) és \(\displaystyle OD\) ívek egyenlők, ezért \(\displaystyle OE\) a \(\displaystyle BED\) szög külső szögfelezője. A külső szögfelezőre merőleges, a szög csúcsán átmenő \(\displaystyle AEC\) egyenes tehát a \(\displaystyle BED\) szög belső szögfelezője.

Statistics:

72 students sent a solution.
4 points:	66 students.
3 points:	4 students.
2 points:	1 student.

Problems in Mathematics of KöMaL, December 2024