Problem B. 5431. (January 2025)

B. 5431. Let \(\displaystyle k\) denote the incircle of triangle \(\displaystyle ABC\), and let \(\displaystyle I\) denote its center. Line \(\displaystyle AI\) intersects circle \(\displaystyle k\) in points \(\displaystyle D\) and \(\displaystyle E\) such that \(\displaystyle D\) is closer to \(\displaystyle A\) than \(\displaystyle E\). Let \(\displaystyle k\) be tangent to \(\displaystyle AC\) at \(\displaystyle F\). Let the tangent of \(\displaystyle K\) at point \(\displaystyle E\) intersect \(\displaystyle AC\) at \(\displaystyle G\). Prove that \(\displaystyle GI\) is parallel to \(\displaystyle FD\).

Proposed by: Márton Lovas, Budakalász

(3 pont)

Deadline expired on February 10, 2025.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás.

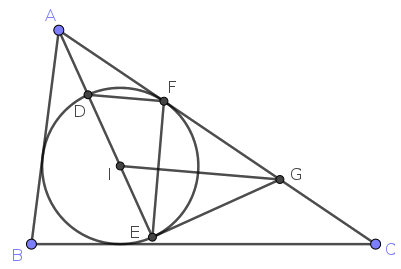
Egyrészt a beírt körnek \(\displaystyle DE\) átmérője, ezért a Thalész-tétel szerint \(\displaystyle EFD \sphericalangle = 90^{\circ}\), azaz \(\displaystyle DF \perp EF\).

Másrészt \(\displaystyle E\) és \(\displaystyle F\), mint a \(\displaystyle G\)-ből a beírt körhöz húzott érintők érintési pontjai a \(\displaystyle GI\) tengelyre nézve egymás tükörképei, tehát \(\displaystyle GI \perp EF\).

Ezzel beláttuk, hogy \(\displaystyle DF\) és \(\displaystyle GI\) is merőleges az \(\displaystyle EF\) egyenesre, tehát egymással párhuzamosak.

Statistics:

83 students sent a solution.
3 points:	69 students.
2 points:	7 students.
1 point:	1 student.
0 point:	3 students.
Not shown because of missing birth date or parental permission:	1 solutions.

Problems in Mathematics of KöMaL, January 2025