Problem B. 5437. (January 2025)

B. 5437. Let \(\displaystyle ABC\) be a triangle satisfying \(\displaystyle BC<AC\), and let \(\displaystyle D\) be a point on side \(\displaystyle AC\) satisfying \(\displaystyle BC=DC\). Let circle \(\displaystyle \Gamma\) be tangent to arc \(\displaystyle AC\) not containing \(\displaystyle B\) of the circumcircle of \(\displaystyle ABC\) at point \(\displaystyle X\), and to line segment \(\displaystyle AC\) at \(\displaystyle D\). Let the tangent line from \(\displaystyle B\) to \(\displaystyle \Gamma\) that is closer to \(\displaystyle C\) intersect \(\displaystyle AC\) at \(\displaystyle Y\), and be tangent to \(\displaystyle \Gamma\) at \(\displaystyle Z\). Prove that if \(\displaystyle A\), \(\displaystyle Y\), \(\displaystyle X\) and the circumcenter of triangle \(\displaystyle ABC\) are concyclic, then \(\displaystyle AZ=CZ\).

Proposed by: Márton Lovas, Budakalász

(6 pont)

Deadline expired on February 10, 2025.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Először megmutatjuk, hogy \(\displaystyle Z\) a \(\displaystyle CX\) szakasz belsejébe esik, és \(\displaystyle AYZX\) húrnégyszög. Ehhez nem lesz szükségünk az \(\displaystyle O\) helyzetére.

Tekintsük a \(\displaystyle C\) középpontú, a \(\displaystyle B,D\) pontokon átmenő körre való inverziót. A különböző objektumokat vesszővel fogjuk jelölni. Világos, hogy \(\displaystyle B'=B\), \(\displaystyle D'=D\), \(\displaystyle (CA)'=CA\) és \(\displaystyle (CX)'=CX\). Mivel \(\displaystyle CD\) a \(\displaystyle D\) pontban érinti \(\displaystyle \Gamma\)-t, \(\displaystyle \Gamma'=\Gamma\).

Az \(\displaystyle X'\) pont a \(\displaystyle \Gamma\) kör és a \(\displaystyle CX\) egyenes második, \(\displaystyle X\)-től különböző metszéspontja. Az \(\displaystyle ABCX\) kör átmegy az inverzió pólusán, ezért \(\displaystyle (ABCX)'=BX'\). Mivel az \(\displaystyle ABCX\) kör \(\displaystyle X\)-ben érinti \(\displaystyle \Gamma\)-t, a képeik, a \(\displaystyle BX'\) egyenes és \(\displaystyle \Gamma\) is érintik egymást az \(\displaystyle X'\) pontban.

A \(\displaystyle CX\) szakasz a körülírt kör húrja, ezért mindenképpen elmetszi a \(\displaystyle \Gamma\) kört. Ezért \(\displaystyle BX'\) a \(\displaystyle B\)-ből \(\displaystyle \Gamma\)-hoz húzott, \(\displaystyle C\)-hez közelebbi éríntő, vagyis \(\displaystyle X'=Z\).

Végül, \(\displaystyle Y=BZ\cap AC=(ABCX)'\cap(AC)'=A'\). Az inverzió tulajdonságai miatt az \(\displaystyle A\), \(\displaystyle X\), \(\displaystyle A'=Y\) és \(\displaystyle X'=Z\) pontok egy körön vagy egyenesen vannak, de egyenesre nem eshetnek, mert akkor ez az egyenes tartalmazná az \(\displaystyle A,C,X\) pontokat.

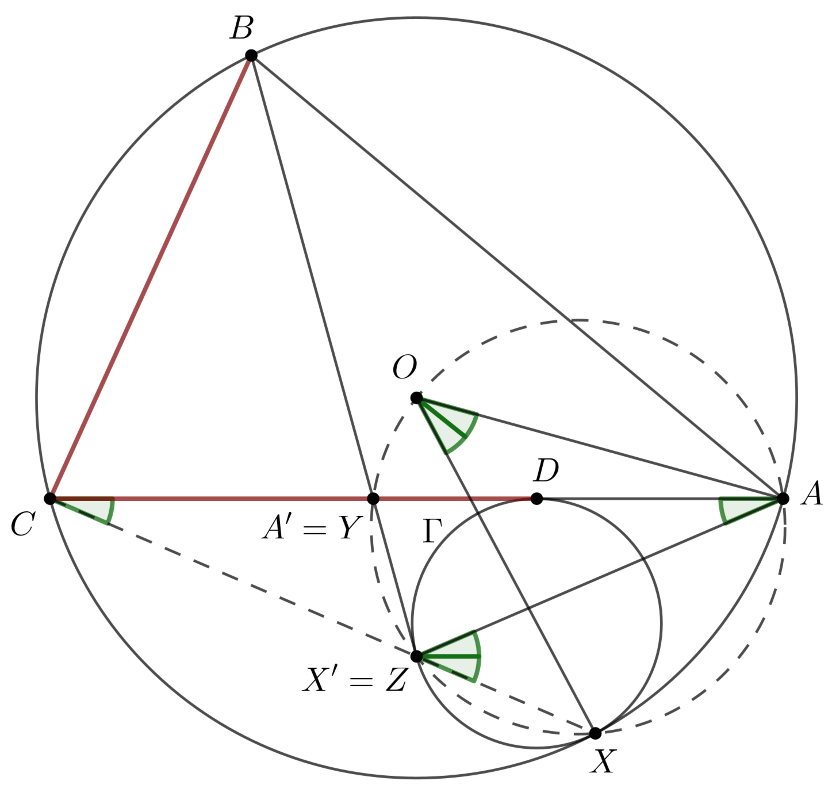
Ezek után, a fentiek és feladat feltételei szerint \(\displaystyle Z\) és \(\displaystyle O\) is az \(\displaystyle AXY\) körön van. Az \(\displaystyle ACZ\) háromszög szögeiből, valamint a kerületi és középponti szögek tételéből

\(\displaystyle ACZ\sphericalangle+ZAC\sphericalangle = AZX\sphericalangle = AOX\sphericalangle = 2ACX\sphericalangle = 2ACZ\sphericalangle, \)

tehát \(\displaystyle ZAC\sphericalangle=ACZ\sphericalangle\), az \(\displaystyle ACZ\) háromszög egyenlő szárú, és \(\displaystyle AZ=CZ\).

Statistics:

16 students sent a solution.
6 points:	Ali Richárd, Bui Thuy-Trang Nikolett, Diaconescu Tashi, Holló Martin, Kovács Benedek Noel, Minh Hoang Tran, Prohászka Bulcsú, Sárdinecz Dóra, Sha Jingyuan, Vigh 279 Zalán, Virág Tóbiás.
4 points:	1 student.
3 points:	1 student.
2 points:	1 student.
1 point:	1 student.
0 point:	1 student.

Problems in Mathematics of KöMaL, January 2025