Problem B. 5460. (April 2025)

B. 5460. In acute triangle \(\displaystyle ABC\) let \(\displaystyle D\), \(\displaystyle E\) and \(\displaystyle F\) denote the feet of the altitudes from \(\displaystyle A\), \(\displaystyle B\) and \(\displaystyle C\), respectively. Let line \(\displaystyle DE\) intersect circle \(\displaystyle ABC\) at points \(\displaystyle G\), \(\displaystyle H\). Similarly, let line \(\displaystyle DF\) intersect circle \(\displaystyle ABC\) at points \(\displaystyle I\), \(\displaystyle J\). Prove that the radical axis of circles \(\displaystyle EIJ\) and \(\displaystyle FGH\) passes through the orthocenter of triangle \(\displaystyle ABC\).

Proposed by: Viktor Csaplár, Bátorkeszi

(6 pont)

Deadline expired on May 12, 2025.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Azt fogjuk igazolni, hogy az \(\displaystyle EIJ\) és az \(\displaystyle FGH\) körök hatványvonala az \(\displaystyle ABC\) háromszög \(\displaystyle AD\) magassága, ezért biztosan átmegy a magasságponton. Ehhez elég ellenőriznünk, hogy az \(\displaystyle A\) és a \(\displaystyle D\) pont is az \(\displaystyle EIJ\) és az \(\displaystyle FGH\) körök hatványvonalán van.

Legyen \(\displaystyle AB\) felezőpontja \(\displaystyle K\), \(\displaystyle AC\) felezőpontja \(\displaystyle L\). Először megmutatjuk, hogy az \(\displaystyle FGH\) kör átmegy a \(\displaystyle K\) ponton, és ha \(\displaystyle K=F\), akkor az \(\displaystyle AB\) oldal ebben a pontban érinti az \(\displaystyle FGH\) kört, és hasonlóan, az \(\displaystyle EIJ\) kör átmegy \(\displaystyle L\)-en, és ha \(\displaystyle L=E\), akkor \(\displaystyle AC\) érinti az \(\displaystyle EIJ\) kört.

Ha \(\displaystyle AC=BC\), akkor a háromszög egyenlő szárú, és az ábra szimmetrikus az \(\displaystyle AB\) felező merőlegesére, és így az \(\displaystyle EIJ\) kör a \(\displaystyle K=F\) felezőpontban érinti az \(\displaystyle AB\) oldalt.

Ha \(\displaystyle AC\ne BC\), akkor \(\displaystyle K\ne F\), és \(\displaystyle DE\) nem párhuzamos \(\displaystyle AB\)-vel, mert az \(\displaystyle ABDE\) húrnégyszög nem lehet szimmetrikus. Legyen \(\displaystyle R\) az \(\displaystyle AB\) és \(\displaystyle DE\) egyenesek metszéspontja. Az \(\displaystyle R\) pontnak a \(\displaystyle DEFKL\) Feuerbach-körre, az \(\displaystyle ABDE\) körre, valamint az \(\displaystyle ABCGHIJ\) körülírt körre vonatkozó hatványából

\(\displaystyle RF \cdot RK = RD \cdot RE = RA \cdot RB = RG \cdot RH, \)

ami mutatja, hogy \(\displaystyle K\), \(\displaystyle F\), \(\displaystyle G\) és \(\displaystyle H\) egy körön van. Hasonlóan láthatjuk, hogy az \(\displaystyle EIJ\) kör átmegy az \(\displaystyle L\) ponton.

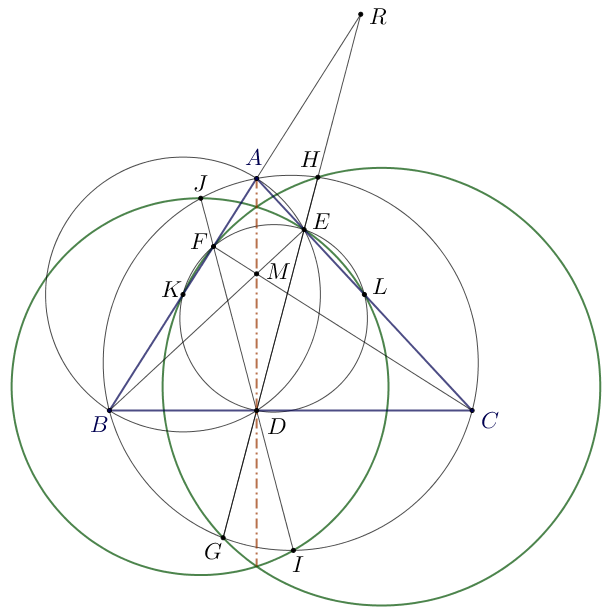
Az \(\displaystyle ABCGHIJ\) körülírt kör és az \(\displaystyle EIJL\) kör hatványvonala a közös \(\displaystyle IJ\) húr, az \(\displaystyle ABCGHIJ\) kör és az \(\displaystyle FGHK\) kör hatványvonala pedig a \(\displaystyle GH\) egyenes. Ezek metszéspontja, \(\displaystyle D\) a három kör hatványpontja, ami rajta van az \(\displaystyle EIJL\) és az \(\displaystyle FGHK\) kör hatványvonalán.

Hasonlóan, a \(\displaystyle DEFKL\) Feuerbach-kör és az \(\displaystyle EIJL\) kör hatványvonala az \(\displaystyle EL\) egyenes, a \(\displaystyle DEFKL\) kör és az \(\displaystyle FGHK\) kör hatványvonala a \(\displaystyle GK\) egyenes, \(\displaystyle A\) a három kör hatványpontja, szintén rajta van az \(\displaystyle EIJL\) és \(\displaystyle FGHK\) körök hatványvonalán.

Ezzel megmutattuk, hogy \(\displaystyle D\) és \(\displaystyle A\), tehát az \(\displaystyle ABC\) háromszög magasságpontja is az \(\displaystyle EIJ\) és az \(\displaystyle FGH\) körök hatványvonalán van.

Statistics:

15 students sent a solution.
6 points:	Ali Richárd, Aravin Peter, Diaconescu Tashi, Gyenes Károly, Holló Martin, Kerekes András, Sárdinecz Dóra, Sha Jingyuan.
5 points:	Bui Thuy-Trang Nikolett, Li Mingdao, Vigh 279 Zalán.
3 points:	1 student.
2 points:	1 student.
0 point:	1 student.

Problems in Mathematics of KöMaL, April 2025