Problem B. 5478. (October 2025)

B. 5478. Let \(\displaystyle S\) denote the centroid of triangle \(\displaystyle ABC\). Let \(\displaystyle T\) denote the foot of the height from vertex \(\displaystyle A\) in triangle \(\displaystyle ABC\). Ray \(\displaystyle TS\) (starting from point \(\displaystyle T\)) intersect the circumcircle of the triangle in \(\displaystyle V\). Prove that \(\displaystyle S\) trisects line segment \(\displaystyle TV\).

Proposed by Viktor Vígh, Sándorfalva

(3 pont)

Deadline expired on November 10, 2025.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Jelölje \(\displaystyle F\) a \(\displaystyle BC\) oldal felezőpontját. Ha a háromszögben \(\displaystyle AB=AC\), akkor a \(\displaystyle T\) és \(\displaystyle F\) pontok egybeesnek, és az \(\displaystyle A\) és \(\displaystyle V\) pontok is azonosak, azaz a \(\displaystyle TV\) szakasz a háromszög \(\displaystyle A=V\) pontból megrajzolt súlyvonala, amit \(\displaystyle S\) valóban harmadol. Tegyük fel a továbbiakban, hogy \(\displaystyle AB \neq AC\), és használjuk az alábbi ábrát és jelöléseit.

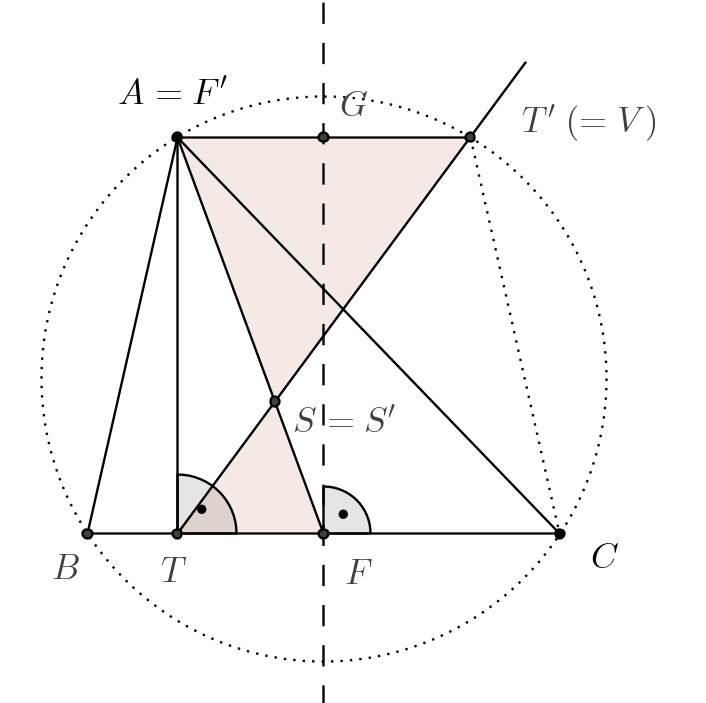
A \(\displaystyle STF\) háromszög képét az \(\displaystyle S\) középpontú \(\displaystyle \lambda=-2\) arányú középpontos hasonlóság mellett jelölje \(\displaystyle S'T'F'\). Nyilván \(\displaystyle S=S'\), továbbá mivel az \(\displaystyle S\) súlypont az \(\displaystyle AT\) súlyvonal \(\displaystyle F\)-hez közelebbi harmadolópontja \(\displaystyle F'=A\).

A középpontos hasonlóság tulajdonságai és aránya alapján \(\displaystyle TF \parallel T'F'=T'A\), és \(\displaystyle T'A=2 \cdot TF\). Jelölje \(\displaystyle G\) a \(\displaystyle T'A\) szakasz felezőpontját. A \(\displaystyle TFGA\) négyszög két szemközti \(\displaystyle TF\) és \(\displaystyle GA\) oldala párhuzamos és egyenlő hosszúságú, azaz \(\displaystyle TFGA\) paralelogramma; továbbá \(\displaystyle ATF \sphericalangle =90^{\circ}\) figyelembevételével \(\displaystyle TFGA\) téglalap. Ebből következik, hogy \(\displaystyle CFG \sphericalangle =90^{\circ}\), azaz \(\displaystyle FG\) egyenese a \(\displaystyle BC\) szakasz felezőmerőlegese. Az eddigiek alapján \(\displaystyle FG\) egyúttal \(\displaystyle AT'\) felezőmerőlegese is, azaz \(\displaystyle BCT'A\) szimmetrikus trapéz, tehát \(\displaystyle B\), \(\displaystyle C\), \(\displaystyle T'\) és \(\displaystyle A\) pontok egy körön vannak, azaz \(\displaystyle T'\) rajta van \(\displaystyle ABC\) körén, és így (\(\displaystyle V\) feladatbeli definíciója miatt) \(\displaystyle T'=V\).

Ez pedig – a hasonlóság \(\displaystyle \lambda=-2\) arányát tekintve – éppen azt jelenti, hogy \(\displaystyle S\) a \(\displaystyle TV\) szakasz (\(\displaystyle T\)-hez közelebbi) harmadolópontja.

Megjegyzés: A háromszög Feuerbach-körének két ismert tulajdonsága (lásd a következő ábra!):

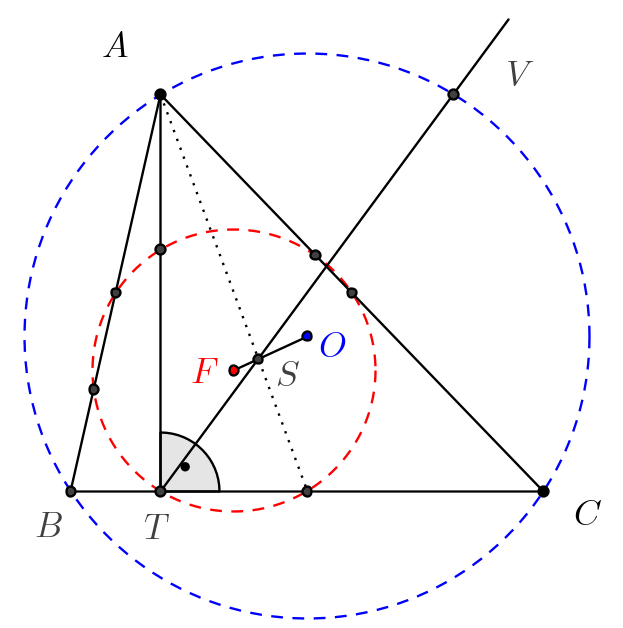
– a Feuerbach-kör sugara feleakkora, mint a háromszög köré írt kör sugara; illetve

– a háromszög \(\displaystyle S\) súlypontja az \(\displaystyle OF\) szakasz \(\displaystyle F\)-hez közelebbi harmadolópontja (ahol \(\displaystyle O\) a háromszög köré írt kör, míg \(\displaystyle F\) (most) a Feuerbach-kör középpontja).

Ezekből azonnal következik, hogy a Feuerbach-körön lévő \(\displaystyle T\) pont \(\displaystyle S\) középpontú \(\displaystyle \lambda=-2\) arányú középpontos hasonlóság melletti \(\displaystyle T'\) képe a háromszög kőré írt körének pontja, azaz \(\displaystyle T'=V\); és így valóban teljesül \(\displaystyle VS=2 \cdot ST\).

Statistics:

77 students sent a solution.
3 points:	63 students.
2 points:	5 students.
1 point:	3 students.
0 point:	5 students.

Problems in Mathematics of KöMaL, October 2025