Problem B. 5483. (October 2025)

B. 5483. A deck of \(\displaystyle 2n\) cards consists of \(\displaystyle n\) suits, each suit consisting of two values, 1 and 2. \(\displaystyle n\) players play the following cooperative game: They start by shuffling the \(\displaystyle 2n\) cards, then each player is dealt two cards, which they reveal to the other players. Subsequently, they decide together the order they sit down around a round table, and they also choose the player starting the game. During the game, each consecutive player (in the clockwise direction) tries to put down a card, however, a card with value 2 can only be put down if the card of the same suit with value 1 is already on the table. They win the game if they manage to put all the cards on the table, however, they lose the game if somebody holding at least one card in their hand cannot put down a card on the table. Prove that the players can always win the game, regardless of the hand they were dealt.

Proposed by Anett Kocsis and András Imolay, Budapest, based on a Dürer competition problem

(5 pont)

Deadline expired on November 10, 2025.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Jelölje \(\displaystyle k\) azon játékosok számát, akik két \(\displaystyle 1\)-es kártyát kaptak (a továbbiakban őket 11-eseknek nevezzük). Mivel ugyanannyi 1-es és 2-es van, ezért ekkor \(\displaystyle k\) olyan játékosnak kell lennie, akik két \(\displaystyle 2\)-es kártyát kaptak (22-esek), míg a maradék \(\displaystyle n-2k\) játékos egy \(\displaystyle 1\)-est és egy \(\displaystyle 2\)-est kapott (12-esek).

Üljenek le a játékosok úgy, hogy először a 11-esek kerüljenek sorra, utána a 12-esek, míg végül a 22-esek (egy-egy csoporton belül a sorrend tetszőleges lehet). A következőkben megmutatjuk, hogy ha ilyen sorrendben ülnek le, akkor (okos választásokkal) le tudják tenni az összes kártyát.

Először a 11-esek tegyenek le egy-egy 1-es kártyát (hogy melyiket a kettő közül, azt később magyarázzuk el). Ezután a 12-esek tegyék le az 1-eseiket. Az első fordulót a 22-esek zárják. Ha ők mindannyian le tudnak tenni egy-egy kártyát, akkor a második fordulóban már nem lehet gond, hiszen mire a második fordulóban először kerül 2-es kártya lerakásra (a sorban először következő 12-es játékosnál), már az összes 1-es kártya le lesz téve.

Tehát csak arra kell figyelnünk, hogy az első fordulóban a 11-esek úgy válasszanak kártyát, hogy az első forduló végén a 22-esek közül mindenki le tudja tenni valamelyik kártyáját.

Készítsünk egy páros gráfot, melynek csúcsainak

• egyik osztálya a 11-es és 12-es halmazának uniója: \(\displaystyle V = \{ v_1, v_2, \ldots, v_{n-k} \}\),
• másik osztálya pedig a 22-es játékosok halmaza: \(\displaystyle W = \{w_1,w_2,\ldots,w_k \}\).

A \(\displaystyle w_i\) csúcsot akkor kötjük össze a \(\displaystyle v_j\) csúccsal, ha a \(\displaystyle w_i\) kezében levő 2-esek közül valamelyiknek az ugyanolyan színű párja \(\displaystyle v_j\) kezében van.

A kapott páros gráfban minden fokszám legfeljebb 2, tehát a gráf utakra és páros körökre bomlik (valójában az utak is mindig páros élből fognak állni, de ennek nincs jelentősége). Hagyjunk el minden második élt a a páros körökből és az utakból alternáló módon, azaz az utaknak az egyik végéről, a köröknek tetszőleges pontjából indulva az első, harmadik, ötödik, stb. éleket megtartva, a második, negyedik, hatodik, stb. éleket elhagyva. Így egy olyan részgráf marad, amelynek minden \(\displaystyle W\)-beli csúcsban pontosan 1, míg minden \(\displaystyle V\)-beli csúcsban legfeljebb 1 a fokszáma, tehát a \(\displaystyle W\) halmazt bepárosítja a \(\displaystyle V\) halmazba.

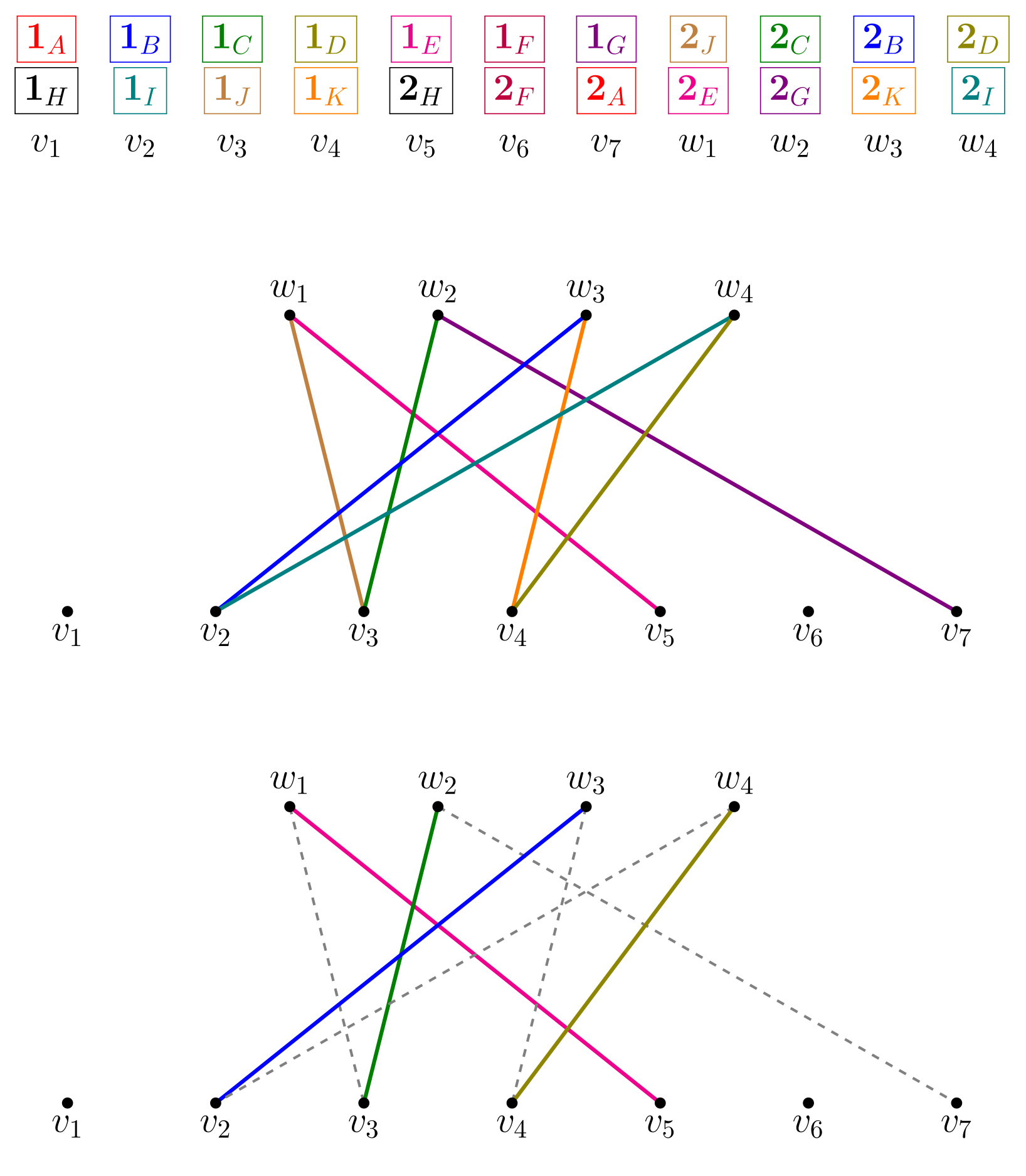
A kapott bepárosítás fogja megadni, hogy miként válasszák ki a 11-es játékosok az elsőként letett kártyájukat. Ha a \(\displaystyle v_i\) jelű 11-es játékos a \(\displaystyle w_j\) jelű 22-esnek a párja a gráfbéli párosítás szerint, akkor \(\displaystyle v_i\)-nek azt a kártyáját kell letennie először, amelyiknek \(\displaystyle w_j\)-nél van az azonos színű párja (esetleg előfordulhat, hogy mindkét \(\displaystyle v_i\)-nél levő kártyának \(\displaystyle w_j\)-nél van a párja – ilyenkor bármelyiket leteheti).

Ezzel garantáljuk, hogy minden 22-es játékos tud lapot tenni az első körben – hiszen mindegyiküknek van egy párja a gráfban, aki biztosítja, hogy legalább az egyik kezükben élevő 2-esnek már le van téve az azonos színű 1-es párja.

Megjegyzés. A páros gráfban a párosítás létezésének bizonyításakor lehet hivatkozni a Kőnig–Hall-tételre is. De mint megmutattuk, igazából nincs szükség a tétel erejére – amennyiben minden fokszám legfeljebb 2, akkor könnyű egy maximális párosítást találni egy páros gráfban.

Megjegyzés. A feladat a Dürer Verseny 2025 februári döntőjén az E kategóriában kitűzött 1b) feladat általánosítása.

Statistics:

100 students sent a solution.
5 points:	73 students.
4 points:	14 students.
3 points:	6 students.
2 points:	2 students.
0 point:	2 students.
Not shown because of missing birth date or parental permission:	2 solutions.

Problems in Mathematics of KöMaL, October 2025