Problem B. 5484. (October 2025)

B. 5484. Let \(\displaystyle M\) denote the orthocenter of acute triangle \(\displaystyle ABC\), and let \(\displaystyle F\) denote the midpoint of side \(\displaystyle BC\). Let \(\displaystyle T\) denote the foot of the perpendicular from \(\displaystyle M\) to the inner angle bisector at vertex \(\displaystyle A\). Line \(\displaystyle FT\) intersects side \(\displaystyle AC\) at point \(\displaystyle D\). Prove that the circumcircle of triangle \(\displaystyle CDF\) contains the foot of the height of triangle \(\displaystyle ABC\) from vertex \(\displaystyle A\).

Proposed by Bálint Bíró, Eger

(6 pont)

Deadline expired on November 10, 2025.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Használjuk az ábra jelöléseit, legyen a \(\displaystyle C\)-ből induló magasság talppontja \(\displaystyle C_0\). Tükrözzük az \(\displaystyle M\) magasságpontot az \(\displaystyle AB\) oldalra, az \(\displaystyle AT\) szögfelezőre és a \(\displaystyle BC\) oldal \(\displaystyle F\) felezőpontjára, és jelölje a tükörképeket rendre \(\displaystyle M_C\), \(\displaystyle M'\) és \(\displaystyle A'\). Jól ismert, hogy \(\displaystyle M_C\) és \(\displaystyle A'\) az \(\displaystyle ABC\) háromszög körülírt körén van, és \(\displaystyle A'\) éppen a kör \(\displaystyle A\)-val átellenes pontja, azaz \(\displaystyle AA'\) átmérő (lásd pl. itt és itt).

Szintén közismert, hogy az \(\displaystyle AT\) szögfelező felezi az \(\displaystyle AA'\) átmérő és \(\displaystyle AM\) magasságok szögét (lásd pl. 2. segédtétel itt). Ebből következik, hogy az \(\displaystyle M'\) tükörkép illeszkedik \(\displaystyle AA'\)-re.

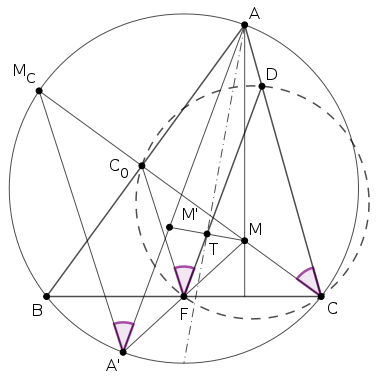
Vegyük észre, hogy a tükrözések miatt \(\displaystyle TF\) középvonal az \(\displaystyle MM'A'\) háromszögben, azaz \(\displaystyle TF\parallel A'M'\), másképpen írva \(\displaystyle DF\parallel AA'\).

Ugyanígy \(\displaystyle C_0F\) középvonal az \(\displaystyle MM_CA'\) háromszögben, ezért \(\displaystyle FC_0\parallel A'M_C\). Így \(\displaystyle DFC_0\sphericalangle = AA'M_C\sphericalangle\), hiszen párhuzamos szárú szögek.

Másrészt az \(\displaystyle ABC\) körben azonos íven nyugvó kerületi szögek, tehát \(\displaystyle AA'M_C\sphericalangle = ACM_C\sphericalangle = DCC_0\sphericalangle \). Kaptuk, hogy \(\displaystyle DFC_0\sphericalangle=DCC_0\sphericalangle\), azaz \(\displaystyle F\) és \(\displaystyle C\) a \(\displaystyle C_0D\) ugyanazon látókörívén van, amiből az állítás következik.

Diszkusszió: Világos, hogy \(\displaystyle M\) és \(\displaystyle T\) az \(\displaystyle ABC\triangle\) belső pontjai. Vegyük észre, hogy a \(\displaystyle BCC_0\) derékszögű háromszög átfogójának felezőpontja \(\displaystyle F\), így \(\displaystyle BFC_0\sphericalangle=2BCC_0\sphericalangle\). Így – felhasználva a megoldásban leírtakat is – következik, hogy \(\displaystyle BFT\sphericalangle>BCA\sphericalangle\), tehát \(\displaystyle D\) pont létezik, és a \(\displaystyle C\) kezdőpontú, \(\displaystyle A\)-t tartalmazó félegyenesen van.

Statistics:

Problem B. 5484. is not processed yet.

Problems in Mathematics of KöMaL, October 2025