 Problem C. 1186. (October 2013)
Problem C. 1186. (October 2013)
C. 1186. The lengths of the medians drawn from vertices A and B of triangle ABC are both 6, and the median from A encloses an angle of 60o with side BC. How long are the sides of triangle ABC?
(5 pont)
Deadline expired on November 11, 2013.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Jelölje a \(\displaystyle BC\) és az \(\displaystyle AC\) oldal felezőpontját rendre \(\displaystyle F_A\), illetve \(\displaystyle F_B\). Két eset van: 1. eset, ha \(\displaystyle AF_AB\angle=60^{\circ}\); 2. eset, ha \(\displaystyle CF_AA\angle=60^{\circ}\). Mindkét esetben \(\displaystyle F_AF_B||AB\) és \(\displaystyle F_BB=F_AA\), tehát \(\displaystyle ABF_AF_B\) húrtrapéz, így szárait összekötve egyenlő szárú háromszöget kapunk. tehát az \(\displaystyle ABC\) háromszög egyenlő szárú, szárának hossza legyen \(\displaystyle a\).
Mivel a súlyvonalak harmadolják egymást, és mindkét súlyvonal hossza 6, így \(\displaystyle SF_A=SF_B=2\) és \(\displaystyle AS=BS=4\).
1. eset
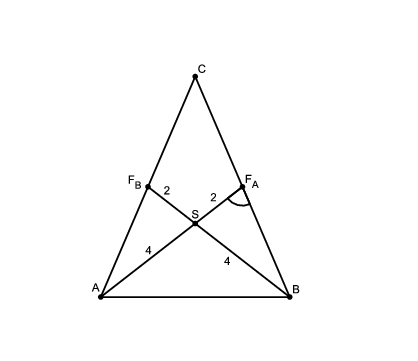
Írjuk fel a koszinusz-tételt az \(\displaystyle SF_AB\) háromszögre:
\(\displaystyle 4^2=2^2+(a/2)^2-2\cdot2\cdot(a/2)\cos60^{\circ},\)
amiből \(\displaystyle \cos60^{\circ}=0,5\) felhasználásával
\(\displaystyle 0=a^2-4a-48.\)
Ennek megoldása:
\(\displaystyle a_{1,2}=\frac{4\pm\sqrt{208}}{2}.\)
Mivel \(\displaystyle a\) pozitív, ezért az egyetlen megoldás \(\displaystyle a=2+2\sqrt{13}\approx9,21\) és ebből \(\displaystyle a/2\approx4,61\).
Írjuk fel a koszinusz-tételt az \(\displaystyle AF_AB\) háromszögre:
\(\displaystyle c^2=6^2+4,61^2-2\cdot6\cdot4,61\cdot\cos60^{\circ},\)
\(\displaystyle c^2=29,5921,\)
amiből \(\displaystyle c>0\) miatt \(\displaystyle c\approx5,44\) következik.
Tehát a háromszög oldalai ebben az esetben: \(\displaystyle AC=BC=9,21\) és \(\displaystyle AB=5,44\).
2. eset
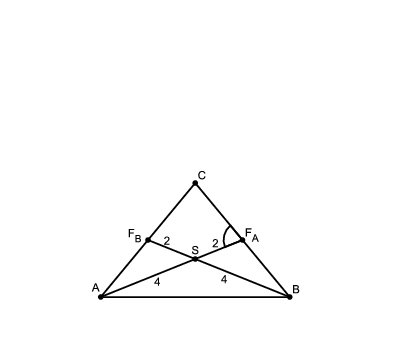
Ekkor \(\displaystyle SF_AB\angle=120^{\circ}\). Írjuk fel a koszinusz-tételt az \(\displaystyle SF_AB\) háromszögre:
\(\displaystyle 4^2=2^2+(a/2)^2-2\cdot2\cdot(a/2)\cos120^{\circ},\)
amiből \(\displaystyle \cos120^{\circ}=-0,5\) felhasználásával
\(\displaystyle 0=a^2+4a-48.\)
Ennek megoldása:
\(\displaystyle a_{1,2}=\frac{-4\pm\sqrt{208}}{2}.\)
Mivel \(\displaystyle a\) pozitív, ezért az egyetlen megoldás \(\displaystyle a=-2+2\sqrt{13}\approx5,21\) és ebből \(\displaystyle a/2\approx2,61\).
Írjuk fel a koszinusz-tételt az \(\displaystyle AF_AB\) háromszögre:
\(\displaystyle c^2=6^2+2,61^2-2\cdot6\cdot2,61\cdot\cos120^{\circ},\)
\(\displaystyle c^2=58,4721,\)
amiből \(\displaystyle c>0\) miatt \(\displaystyle c\approx7,65\) következik.
Tehát a háromszög oldalai ebben az esetben: \(\displaystyle AC=BC=5,21\) és \(\displaystyle AB=7,65\).
Statistics:
200 students sent a solution. 5 points: Barna Kinga, Bekő Zsófia, Bereczki Zoltán, Bottlik Judit, Cserna Balázs, Denke Dorottya, Fényes Balázs, Fülöp Erik, Harangozó Ákos, Horváth 016 Gábor, Horváth András János, Kardos Bálint Tamás, Kocsis Júlia, Kohlmann Dániel, Laczkó Adrienn, Mályusz Attila, Polgár Márton, Sándor Gergely, Sebők Bence, Szabó 524 Tímea, Szász Róbert, Széles Katalin, Telek Máté László, Zsiros Ádám. 4 points: Bekő Mária, Brányi Balázs, Csahók Tímea, Hegyesi János Géza, Horváth 501 Cintia, Jakab Richárd, Jójárt Alexandra, Kasza Bence, Kerekes Anna, Kis 913 Levente, Klász Viktória, Knoch Júlia, Kósa Szilárd, Matusek Márton, Molnár-Sáska Zoltán, Nagy 911 Viktória, Nguyen Anh Tuan, Papp 535 Ágnes, Paulovics Zoltán, Rimóczi Alma, Szőke Tamás, Temesvári Fanni, Varsányi András. 3 points: 87 students. 2 points: 30 students. 1 point: 19 students. 0 point: 12 students. Unfair, not evaluated: 5 solutionss.
Problems in Mathematics of KöMaL, October 2013
