 Problem C. 1193. (November 2013)
Problem C. 1193. (November 2013)
C. 1193. An isosceles triangle of apex angle 120o is drawn on each side of a unit square, on the outside of the square. An equilateral octagon is obtained. In comparison, consider the regular octagon in which the side of the square formed by connecting every other vertex is unity. Find the ratio of the area of the equilateral octagon to the area of the regular octagon.
(5 pont)
Deadline expired on December 10, 2013.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Egy \(\displaystyle 120^{\circ}\)-os szárszögű egyenlő szárú háromszög alapon fekvő szögei \(\displaystyle 30^{\circ}\)-osak. Így az egyenlő oldalú nyolcszög oldalainak hossza pl. az \(\displaystyle ACF\) derékszögű háromszögből számolható: \(\displaystyle \cos30^{\circ}=AF/AC\), vagyis \(\displaystyle \sqrt3/2=(1/2)/AC\), amiből \(\displaystyle AC=1/\sqrt3\).
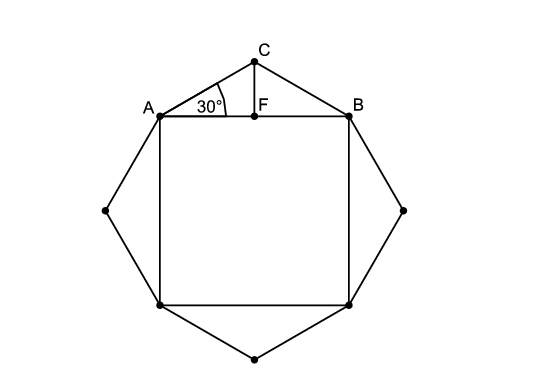
A nyolcszög területe az 1 oldalú négyzet és négy, az \(\displaystyle ABC\) háromszöggel egybevágó háromszög területének összegeként áll elő:
\(\displaystyle T_1=1+4\cdot1/2\cdot(1/\sqrt3)^2\cdot\sin120^{\circ}= 1+4\cdot1/2\cdot(1/3)\cdot(\sqrt3/2)=1+\sqrt3/3.\)
A szabályos nyolcszög köré írt kör sugara az egységoldalú négyzet átlójának fele, vagyis \(\displaystyle \sqrt2/2\). A nyolcszög területe megkapható nyolc egyenlő szárú háromszög területének összegeként:
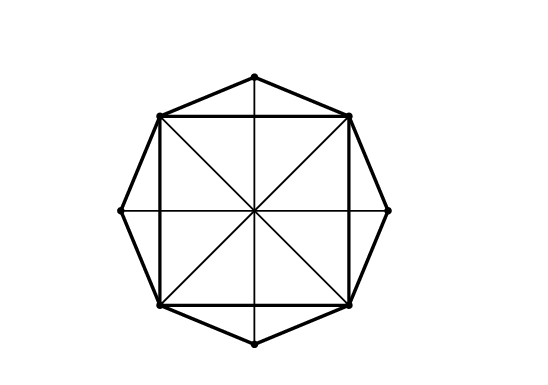
\(\displaystyle T_2=8\cdot1/2\cdot(\sqrt2/2)^2\cdot\sin45^{\circ}=\)
\(\displaystyle =8\cdot1/2\cdot2/4\cdot\sqrt2/2=\sqrt2.\)
A keresett arány:
\(\displaystyle \frac{T_1}{T_2}=\frac{1+\frac{\sqrt3}{3}}{\sqrt2}=\frac{3\sqrt2+\sqrt6}{6}\approx1,12.\)
Statistics:
200 students sent a solution. 5 points: 110 students. 4 points: 46 students. 3 points: 24 students. 2 points: 7 students. 1 point: 1 student. 0 point: 6 students. Unfair, not evaluated: 6 solutionss.
Problems in Mathematics of KöMaL, November 2013
