Problem C. 1208. (January 2014)

C. 1208. The vertices of the parallelograms PQRL and LSTA in the plane are labelled in the same sense around the clock. The parallelograms do not have a point in common, except L. Prove that there exists a pentagon ABCDE (degenerated cases are allowed) in the plane such that the midpoints of the sides are P, Q, R, S, T, in this order.

(5 pont)

Deadline expired on February 10, 2014.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. A bizonyításhoz kihasználjuk a vektorokra vonatkozó paralelogramma szabályt, amely miatt \(\displaystyle \overrightarrow{LQ}=\overrightarrow{LP}+\overrightarrow{LR}\), illetve \(\displaystyle \overrightarrow{LT}=\overrightarrow{LA}+\overrightarrow{LS}\).

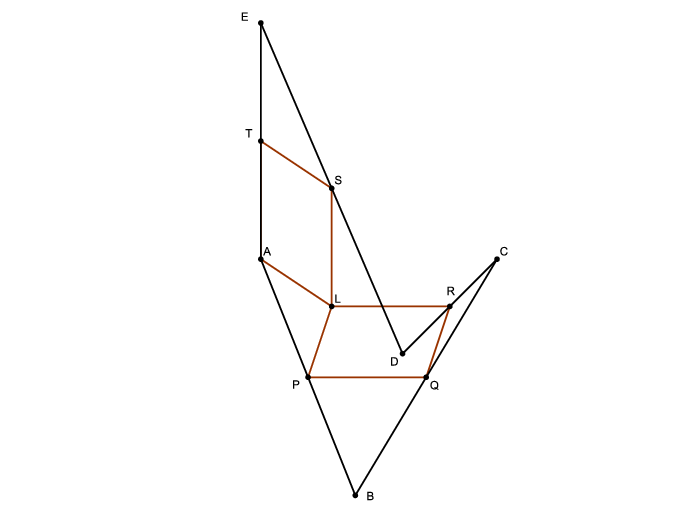
Felhasználjuk még, hogy az \(\displaystyle \overrightarrow{a}\) és \(\displaystyle \overrightarrow{b}\) vektor felezőpontjába mutató \(\displaystyle \overrightarrow{v}\) vektorra \(\displaystyle \overrightarrow{v}=\frac{\overrightarrow{a}+\overrightarrow{b}}{2}\), amiből \(\displaystyle \overrightarrow{b}=2\overrightarrow{v}-\overrightarrow{a}\).

Azt fogjuk bizonyítani, hogy az \(\displaystyle A\) pontot sorra tükrözve a \(\displaystyle P\), \(\displaystyle Q\), \(\displaystyle R\), \(\displaystyle S\) és \(\displaystyle T\) pontokra, az utolsó tükörkép maga az \(\displaystyle A\) pont lesz.

Jelölje tehát az \(\displaystyle A\) pont tükörképét a \(\displaystyle P\) pontra \(\displaystyle B\). Ekkor \(\displaystyle \overrightarrow{LB}=2\overrightarrow{LP}-\overrightarrow{LA}.\)

A \(\displaystyle B\) pont tükörképe a \(\displaystyle Q\) pontra legyen \(\displaystyle C\). Ekkor \(\displaystyle \overrightarrow{LC}=2\overrightarrow{LQ}-\overrightarrow{LB}= 2(\overrightarrow{LP}+\overrightarrow{LR})-(2\overrightarrow{LP}-\overrightarrow{LA}) =2\overrightarrow{LR}+\overrightarrow{LA}\).

A \(\displaystyle C\) pont tükörképe az \(\displaystyle R\) pontra legyen \(\displaystyle D\). Ekkor \(\displaystyle \overrightarrow{LD}=2\overrightarrow{LR}-\overrightarrow{LC}= 2\overrightarrow{LR}-(2\overrightarrow{LR}+\overrightarrow{LA})=-\overrightarrow{LA}\).

A \(\displaystyle D\) pont tükörképe az \(\displaystyle S\) pontra legyen \(\displaystyle E\). Ekkor \(\displaystyle \overrightarrow{LE}=2\overrightarrow{LS}-\overrightarrow{LD}=2\overrightarrow{LS}+\overrightarrow{LA}\).

Végül az \(\displaystyle E\) pont tükörképét a \(\displaystyle T\) pontra jelölje \(\displaystyle F\). Ekkor \(\displaystyle \overrightarrow{LF}=2\overrightarrow{LT}-\overrightarrow{LE}= 2(\overrightarrow{LA}+\overrightarrow{LS})-(2\overrightarrow{LS}+\overrightarrow{LA})=\overrightarrow{LA}\).

Vagyis \(\displaystyle \overrightarrow{LF}=\overrightarrow{LA}\), és így valóban \(\displaystyle F\equiv A\), tehát az így kapott \(\displaystyle ABCDE\) ötszög megfelelő.

Statistics:

20 students sent a solution.
5 points:	Bereczki Zoltán, Farkas Dóra, Fényes Balázs, Gnandt Balázs, Hegel Patrik, Jójárt Alexandra, Telek Máté László.
4 points:	Chourfi Abdel Karim, Demeter Dániel, Hegyesi János Géza, Szabó 524 Tímea, Temesvári Fanni.
3 points:	4 students.
2 points:	1 student.
0 point:	3 students.

Problems in Mathematics of KöMaL, January 2014