 Problem C. 1381. (November 2016)
Problem C. 1381. (November 2016)
C. 1381. Let \(\displaystyle M\) denote the intersection of the line of the altitude drawn from vertex \(\displaystyle A\) of an acute-angled triangle \(\displaystyle ABC\) with the Thales' circle of \(\displaystyle BC\). Let \(\displaystyle N\) be the intersection of the altitude from vertex \(\displaystyle C\) with the Thales' circle of \(\displaystyle AB\). Prove that \(\displaystyle |BM|=|BN|\).
(5 pont)
Deadline expired on December 12, 2016.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Használjuk az 1. ábra jelöléseit. Tekintsük először a Thalész köröknek a háromszög belseje felé eső félköreit. Jelölje \(\displaystyle D\) az \(\displaystyle A\), \(\displaystyle E\) pedig a \(\displaystyle C\) csúcsból induló magasságnak rendre a \(\displaystyle BC\), illetve az \(\displaystyle AB\) oldallal vett metszéspontját. Mivel ekkor a \(\displaystyle D\), illetve az \(\displaystyle E\) csúcsnál jelölt szögek derékszögek, így a Thalész-tétel megfordítása szerint a két pont illeszkedik a megfelelő Thalész-körre.
A Thalész-tétel miatt az \(\displaystyle M\), \(\displaystyle N\) csúcsoknál jelölt szögek is derékszögek. A \(\displaystyle BADΔ\) és a \(\displaystyle BCEΔ\) hasonló, mivel egy-egy szögük derékszög, valamint a \(\displaystyle B\) csúcsnál található szögük közös. Emiatt a megfelelő oldalak aránya megegyezik:
\(\displaystyle \frac{EB}{BC}=\frac{BD}{AB}.\)
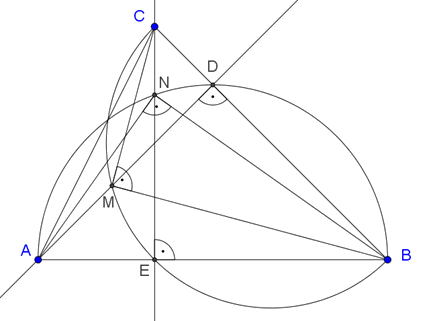
1. ábra
Szorozzunk be a nevezőkkel:
\(\displaystyle EB⋅AB=BD\cdot BC.\)
A derékszögű háromszögekre érvényes befogótételt írjuk fel a \(\displaystyle BMCΔ\)-re és a \(\displaystyle BNAΔ\)-re:
\(\displaystyle BM^2=BD\cdot BC,\)
\(\displaystyle BN^2=EB\cdot AB.\)
Helyettesítsük be az előző egyenlőségbe:
\(\displaystyle BN^2=BM^2, \)
amiből
\(\displaystyle BN=BM.\)
Ezzel az állítást igazoltuk.
Tekintsük most a teljes Thalész köröket a 2. ábra jelöléseit használva.
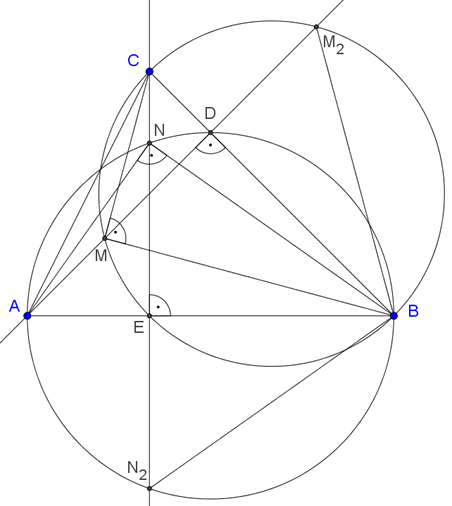
2. ábra
Ekkor mindkét magasságvonal két pontban metszi a megfelelő Thalész kört, ezek \(\displaystyle M\) és \(\displaystyle M_2\), valamint \(\displaystyle N\) és \(\displaystyle N_2\). A \(\displaystyle BC\) oldal fölé emelt Thalész-körnek \(\displaystyle BC\) átmérője, \(\displaystyle AD\) pedig erre merőleges szelő, így \(\displaystyle MM_2\) a \(\displaystyle BC\)-re merőleges húr. Így az \(\displaystyle M\) pont tükörképe \(\displaystyle BC\)-re az \(\displaystyle M_2\) pont.
Tehát \(\displaystyle BM=BM_2\).
Hasonlóan belátható, hogy \(\displaystyle BN=BN_2\). Már tudjuk, hogy \(\displaystyle BN=BM\), így \(\displaystyle BN_2=BM_2=BN=BM\) is igaz.
Statistics:
101 students sent a solution. 5 points: Agócs Katinka, Ajtai Boglárka, Almási Adél Csilla, Dézsi Viktória, Kocsis Júlia, Kovács 161 Márton Soma, Németh Csilla Márta, Takács 666 Réka. 4 points: 55 students. 3 points: 6 students. 2 points: 5 students. 1 point: 7 students. 0 point: 19 students. Unfair, not evaluated: 1 solutions.
Problems in Mathematics of KöMaL, November 2016
