 |
A C. 1431. feladat (2017. szeptember) |
C. 1431. Egy trapéz rövidebb alapjának, egyik, majd másik szárának, végül hosszabbik alapjának hossza ebben a sorrendben egy számtani sorozat egymást követő tagjai. Mekkora a sorozat differenciája, ha a legrövidebb oldal 3 cm, és a hosszabbik alapon fekvő egyik szög 60 fok?
(5 pont)
A beküldési határidő 2017. október 10-én LEJÁRT.
Megoldás. Az 1. megoldáshoz lényegében csak a Pitagorasz-tétel ismeretére van szükség, a 2. megoldás használja a koszinusz-tételt.
1. megoldás. Első esetben legyen az alap és a rövidebbik szár szöge \(\displaystyle 60°\). Használjuk az 1. ábra jelöléseit. Legyen a sorozat differenciája \(\displaystyle d>0\), \(\displaystyle BC=3,\, AB=3+d,\, CD=3+2d,\, AD=3+3d,\, BE=CF=m\).
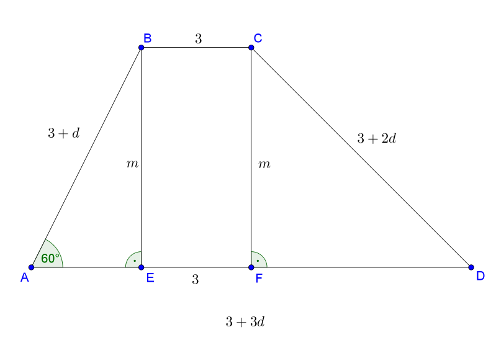
1. ábra
Az \(\displaystyle ABE\) derékszögű háromszögben az A csúcsnál lévő szög \(\displaystyle 60°\), ezért \(\displaystyle AE=\frac{3+d}{2}\).
A \(\displaystyle BEFC\) téglalapban \(\displaystyle EF=BC=3\). \(\displaystyle FD=AD-AE-EF\), vagyis \(\displaystyle FD=3+3d-\frac{3+d}{2}-3=\frac{5d-3}{2}\).
Írjuk fel a Pitagorasz-tételt az \(\displaystyle ABE\) és \(\displaystyle CDF\) derékszögű háromszögekre:
\(\displaystyle m^2=(3+d)^2-\left(\frac{3+d}{2}\right)^2,\)
\(\displaystyle m^2=(3+2d)^2-\left(\frac{5d-3}{2}\right)^2.\)
A jobb oldalak egyenlőségéből a zárójelek felbontása és rendezés után kapjuk, hogy \(\displaystyle d=5\). Ekkor a trapéz oldalai: 3, 8, 13 és 18.
A második esetben legyen az alap és a hosszabbik szár szöge \(\displaystyle 60°\). Használjuk a 2. ábra jelöléseit. Legyen a sorozat differenciája \(\displaystyle d>0\), \(\displaystyle BC=3,\, AB=3+d,\, CD=3+2d,\, AD=3+3d,\, BE=CF=m\).
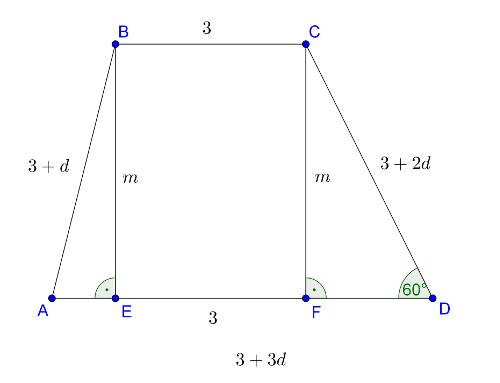
2. ábra
Az \(\displaystyle CDF\) derékszögű háromszögben az \(\displaystyle D\) csúcsnál lévő szög \(\displaystyle 60°\), ezért \(\displaystyle FD=\frac{3+2d}{2}\).
\(\displaystyle AE=AD-EF-FD\), \(\displaystyle AE=3+3d-3-\frac{3+2d}{2}=\frac{4d-3}{2}\).
Írjuk fel a Pitagorasz-tételt az \(\displaystyle ABE\) és \(\displaystyle CDF\) derékszögű háromszögekre:
\(\displaystyle m^2=(3+d)^2-\left(\frac{4d-3}{2}\right)^2,\)
\(\displaystyle m^2=(3+2d)^2-\left(\frac{3+2d}{2}\right)^2.\)
A jobb oldalak egyenlőségéből a zárójelek felbontása és rendezés után kapjuk, hogy \(\displaystyle d=0,5\). Így a trapéz oldalai: 3, 3,5, 4 és 4,5.
Ekkor azonban \(\displaystyle AE=AD-EF-FD=4,5-3-2=-0,5\). Ez úgy lehetséges, hogy a trapéz \(\displaystyle A\) csúcsánál tompaszög van és az \(\displaystyle A\) pont az \(\displaystyle EF\) szakasz belsejébe esik (3. ábra).
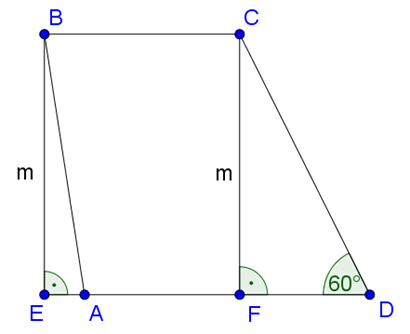
3. ábra
2. megoldás. Húzzunk párhuzamost a rövidebbik szárral a rövidebb oldal másik végpontjában. Így egy paralelogramma és egy háromszög keletkezik.
1. eset: a 60 fokos szög a rövidebbik szárnál van.
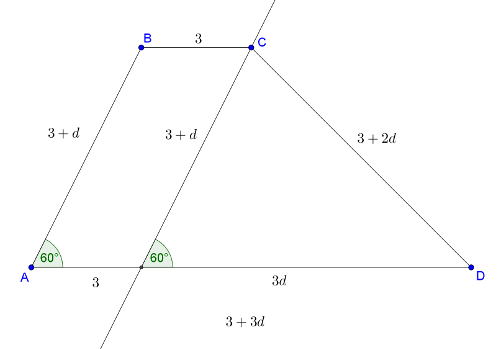
A háromszög 60 fokos oldalával szemközti élre (ami a trapéz hosszabbik szára) felírva a koszinusz-tételt:
\(\displaystyle (3+2d)^2=(3+d)^2+(3d)^2-2\cdot(3+d)\cdot3d\cdot\cos60^{\circ},\)
\(\displaystyle 9+4d^2+12d=9+d^2+6d+9d^2-9d-3d^2,\)
\(\displaystyle 0=3d^2-15d=3d(d-5).\)
Tehát ekkor \(\displaystyle d=5\).
2. eset: a 60 fokos szög a hosszabbik szárnál van.
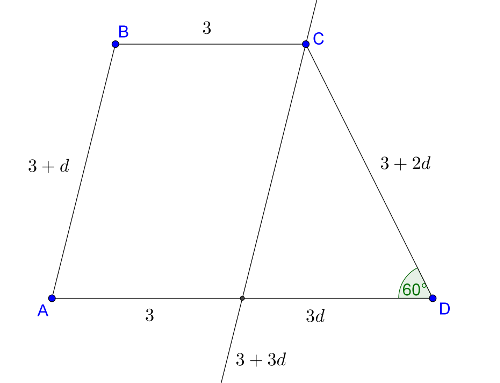
A háromszög 60 fokos oldalával szemközti élre (aminek hossza a trapéz rövidebbik szárának hosszával egyezik meg) felírva a koszinusz-tételt:
\(\displaystyle (3+d)^2=(3+2d)^2+(3d)^2-2\cdot(3+2d)\cdot(3d)\cdot\cos60^{\circ},\)
\(\displaystyle 9+d^2+6d=9+4d^2+12d+9d^2-9d-6d^2,\)
\(\displaystyle 0=6d^2-3d=3d(2d-1).\)
Ekkor \(\displaystyle d=0,5\).
Statisztika:
214 dolgozat érkezett. 5 pontot kapott: 81 versenyző. 4 pontot kapott: 31 versenyző. 3 pontot kapott: 46 versenyző. 2 pontot kapott: 16 versenyző. 1 pontot kapott: 24 versenyző. 0 pontot kapott: 16 versenyző.
A KöMaL 2017. szeptemberi matematika feladatai

