 Problem C. 1431. (September 2017)
Problem C. 1431. (September 2017)
C. 1431. The lengths of the shorter base of a trapezium, then one leg, then the other leg and finally the longer base, in this order, form an arithmetic progression. Given that the length of the shortest side is 3 cm, and one of the angles lying on the longer base is 60 degrees, what is the common difference of the arithmetic progression?
(5 pont)
Deadline expired on October 10, 2017.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Az 1. megoldáshoz lényegében csak a Pitagorasz-tétel ismeretére van szükség, a 2. megoldás használja a koszinusz-tételt.
1. megoldás. Első esetben legyen az alap és a rövidebbik szár szöge \(\displaystyle 60°\). Használjuk az 1. ábra jelöléseit. Legyen a sorozat differenciája \(\displaystyle d>0\), \(\displaystyle BC=3,\, AB=3+d,\, CD=3+2d,\, AD=3+3d,\, BE=CF=m\).
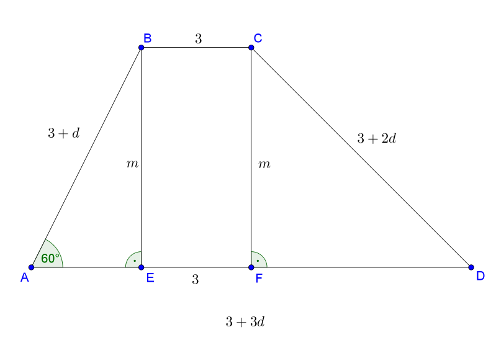
1. ábra
Az \(\displaystyle ABE\) derékszögű háromszögben az A csúcsnál lévő szög \(\displaystyle 60°\), ezért \(\displaystyle AE=\frac{3+d}{2}\).
A \(\displaystyle BEFC\) téglalapban \(\displaystyle EF=BC=3\). \(\displaystyle FD=AD-AE-EF\), vagyis \(\displaystyle FD=3+3d-\frac{3+d}{2}-3=\frac{5d-3}{2}\).
Írjuk fel a Pitagorasz-tételt az \(\displaystyle ABE\) és \(\displaystyle CDF\) derékszögű háromszögekre:
\(\displaystyle m^2=(3+d)^2-\left(\frac{3+d}{2}\right)^2,\)
\(\displaystyle m^2=(3+2d)^2-\left(\frac{5d-3}{2}\right)^2.\)
A jobb oldalak egyenlőségéből a zárójelek felbontása és rendezés után kapjuk, hogy \(\displaystyle d=5\). Ekkor a trapéz oldalai: 3, 8, 13 és 18.
A második esetben legyen az alap és a hosszabbik szár szöge \(\displaystyle 60°\). Használjuk a 2. ábra jelöléseit. Legyen a sorozat differenciája \(\displaystyle d>0\), \(\displaystyle BC=3,\, AB=3+d,\, CD=3+2d,\, AD=3+3d,\, BE=CF=m\).
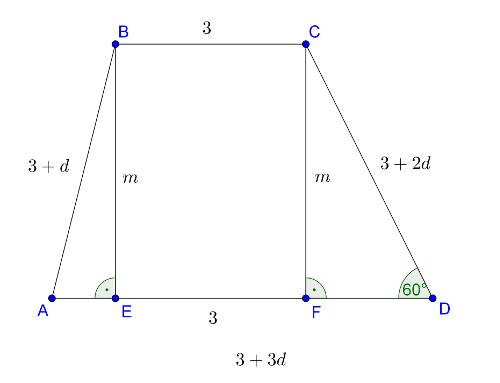
2. ábra
Az \(\displaystyle CDF\) derékszögű háromszögben az \(\displaystyle D\) csúcsnál lévő szög \(\displaystyle 60°\), ezért \(\displaystyle FD=\frac{3+2d}{2}\).
\(\displaystyle AE=AD-EF-FD\), \(\displaystyle AE=3+3d-3-\frac{3+2d}{2}=\frac{4d-3}{2}\).
Írjuk fel a Pitagorasz-tételt az \(\displaystyle ABE\) és \(\displaystyle CDF\) derékszögű háromszögekre:
\(\displaystyle m^2=(3+d)^2-\left(\frac{4d-3}{2}\right)^2,\)
\(\displaystyle m^2=(3+2d)^2-\left(\frac{3+2d}{2}\right)^2.\)
A jobb oldalak egyenlőségéből a zárójelek felbontása és rendezés után kapjuk, hogy \(\displaystyle d=0,5\). Így a trapéz oldalai: 3, 3,5, 4 és 4,5.
Ekkor azonban \(\displaystyle AE=AD-EF-FD=4,5-3-2=-0,5\). Ez úgy lehetséges, hogy a trapéz \(\displaystyle A\) csúcsánál tompaszög van és az \(\displaystyle A\) pont az \(\displaystyle EF\) szakasz belsejébe esik (3. ábra).
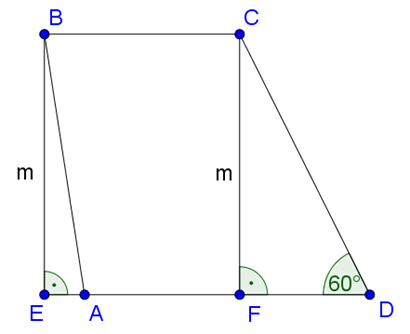
3. ábra
2. megoldás. Húzzunk párhuzamost a rövidebbik szárral a rövidebb oldal másik végpontjában. Így egy paralelogramma és egy háromszög keletkezik.
1. eset: a 60 fokos szög a rövidebbik szárnál van.
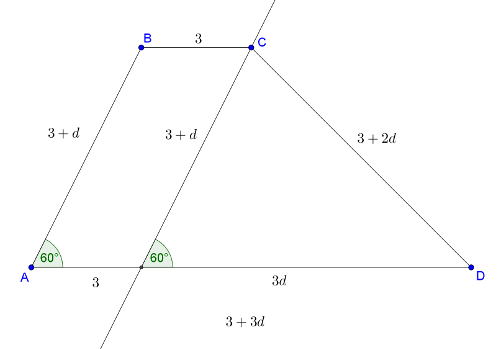
A háromszög 60 fokos oldalával szemközti élre (ami a trapéz hosszabbik szára) felírva a koszinusz-tételt:
\(\displaystyle (3+2d)^2=(3+d)^2+(3d)^2-2\cdot(3+d)\cdot3d\cdot\cos60^{\circ},\)
\(\displaystyle 9+4d^2+12d=9+d^2+6d+9d^2-9d-3d^2,\)
\(\displaystyle 0=3d^2-15d=3d(d-5).\)
Tehát ekkor \(\displaystyle d=5\).
2. eset: a 60 fokos szög a hosszabbik szárnál van.
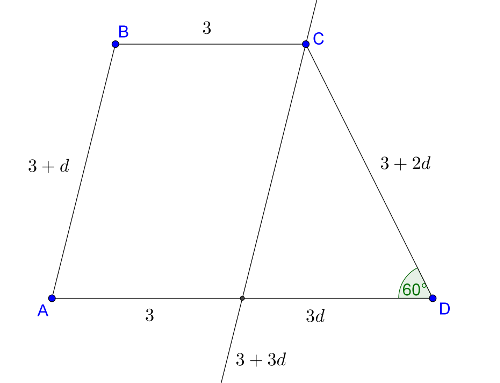
A háromszög 60 fokos oldalával szemközti élre (aminek hossza a trapéz rövidebbik szárának hosszával egyezik meg) felírva a koszinusz-tételt:
\(\displaystyle (3+d)^2=(3+2d)^2+(3d)^2-2\cdot(3+2d)\cdot(3d)\cdot\cos60^{\circ},\)
\(\displaystyle 9+d^2+6d=9+4d^2+12d+9d^2-9d-6d^2,\)
\(\displaystyle 0=6d^2-3d=3d(2d-1).\)
Ekkor \(\displaystyle d=0,5\).
Statistics:
214 students sent a solution. 5 points: 81 students. 4 points: 31 students. 3 points: 46 students. 2 points: 16 students. 1 point: 24 students. 0 point: 16 students.
Problems in Mathematics of KöMaL, September 2017
