Problem C. 1435. (October 2017)

C. 1435. Inside a square of side 2 units, semicircles are drawn over two adjacent sides as diameters. What is the radius of the circle that touches one semicircle and the side of the square internally, and touches the other semicircle externally?

Proposed by D. Fülöp, Pécs

(5 pont)

Deadline expired on November 10, 2017.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Használjuk az ábra jelöléseit. A félkörök sugarai \(\displaystyle R=\frac a2=1\) hosszúak. A kis érintő kör sugara legyen \(\displaystyle r\), a \(\displaystyle HE\) szakasz hossza pedig \(\displaystyle x\). Az érintésekből következik, hogy \(\displaystyle GE=R-r=1-r\), \(\displaystyle GF=R+r=1+r\).

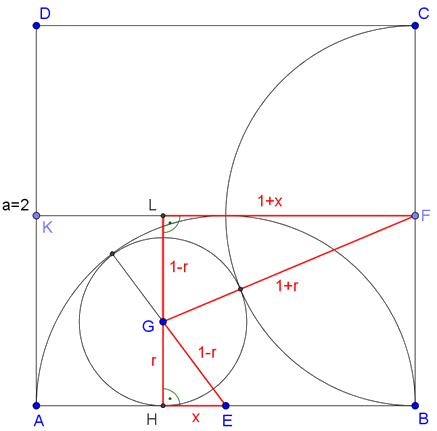
Mivel \(\displaystyle E\), \(\displaystyle F\) és \(\displaystyle K\) a négyzet egy-egy oldalának felezőpontja, és \(\displaystyle HL||BF\), valamint \(\displaystyle KF||AB\), ezért \(\displaystyle GL=R-r=1-r\) és \(\displaystyle FL=R+x=1+x\).

Írjuk fel a Pitagorasz-tételt az \(\displaystyle EGH\) és \(\displaystyle FGL\) derékszögű háromszögekben:

\(\displaystyle (1-r)^2=x^2+r^2,\)

\(\displaystyle (1+r)^2=(1-r)^2+(1+x)^2.\)

Elvégezve a műveleteket és rendezve:

\(\displaystyle 1-x^2=2r,\)

\(\displaystyle 4r=x^2+2x+1.\)

\(\displaystyle 2r\) értékét az első egyenletből a másodikba beírva és rendezve:

\(\displaystyle 2-2x^2=x^2+2x+1,\)

\(\displaystyle 0=3x^2+2x-1.\)

A másodfokú egyenlet pozitív megoldása: \(\displaystyle x=\frac 13\), amiből \(\displaystyle r=\frac{1-x^2}{2}=\frac{1-\frac19}{2}=\frac49\).

A kapott megoldások kielégítik a fenti egyenletrendszert.

Tehát a keresett kör sugara \(\displaystyle r=\frac49\).

Statistics:

101 students sent a solution.
5 points:	69 students.
4 points:	8 students.
3 points:	3 students.
2 points:	4 students.
0 point:	17 students.

Problems in Mathematics of KöMaL, October 2017