 |
A C. 1437. feladat (2017. október) |
C. 1437. Októberi számunkban a feladat hibásan jelent meg. A feladatot újra kitűzzük; a novemberi feladatokkal együtt küldhető be.
Kilenc különböző egyenes mindegyike \(\displaystyle 2:3\) arányban osztja egy négyzet területét úgy, hogy egyik egyenes sem vág le háromszög alakú részt a négyzetből. Igazoljuk, hogy az egyenesek között van három olyan, amelyek egy ponton mennek keresztül.
(5 pont)
A beküldési határidő 2017. december 11-én LEJÁRT.
Megoldás. A feladat állítása akkor igaz, ha feltesszük, hogy az egyenesek mindegyike két trapézra vágja a négyzetet. Legyen \(\displaystyle e\) egy olyan egyenes, amely 2:3 arányban két trapézra osztja az \(\displaystyle ABCD\) négyzet területét.
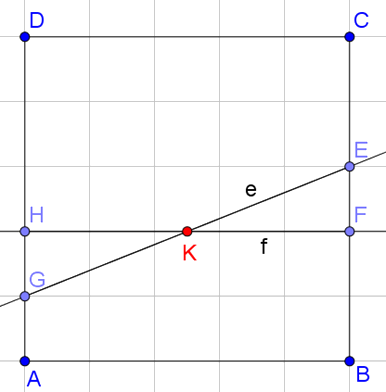
Legyen az \(\displaystyle e\) egyenes négyzetbe eső \(\displaystyle EG\) szakaszának felezőpontja \(\displaystyle K\). Húzzunk a \(\displaystyle K\) ponton keresztül párhuzamost a négyzet \(\displaystyle AB\) oldalával, legyen ez az \(\displaystyle f\) egyenes, metszéspontjai a négyzet \(\displaystyle BC\) és \(\displaystyle AD\) oldalával pedig rendre \(\displaystyle F\) és \(\displaystyle H\). Ekkor a keletkező \(\displaystyle EFK\) és \(\displaystyle HGK\) derékszögű háromszögek egybevágóak lesznek, mert megegyeznek egy oldalban és három szögben. Ezeknek a háromszögeknek a területe is egyenlő, ezért az \(\displaystyle f\) egyenes, vagyis az \(\displaystyle FH\) szakasz is 2:3 arányban osztja az \(\displaystyle ABCD\) négyzet területét.
Ebből az következik, hogyha egy egyenes 2:3 arányban két trapézra osztja a négyzet területét, akkor át kell haladnia egy, a négyzet területét szintén 2:3 arányban osztó, a négyzet két szemközti oldalával párhuzamos szakasz felezőpontján. Ilyen szakasz és felezőpont négy darab van, tehát a skatulyaelv miatt a kilenc különböző, 2:3 arányban osztó egyenes közül háromnak egy ilyen ponton kell átmennie.
Statisztika:
134 dolgozat érkezett. 5 pontot kapott: Agócs Katinka, Almási Adél Csilla, Balog 518 Lóránd, Bukor Benedek, Csóti Kristóf, Dékány Barnabás, Forgács Kata, Gálffy Veronika, Gém Viktória, Hámori Janka, Horváth 31 László, Horváth 999 Anikó, Jankovits András, Kerekes Boldizsár, Kis 194 Károly, Kovács 157 Zita, Kovács 161 Márton Soma, Kovács Fruzsina Dóra, Magyar 257 Boglárka, Makrai-Kis Balázs, Markó Gábor, Mészáros 916 Márton, Mészáros Melinda, Molnár 410 István, Németh Csilla Márta, Rittgasszer Ákos, Rozgonyi Gergely, Sal Dávid, Shuborno Das, Száz Máté, Szécsi Adél Lilla, Szepessy Luca, Szőke Péter, Szőnyi Laura, Tóth 411 Zoltán, Tóth Kristóf ZMG, Tóth Lilla Eszter , Trombitás Karolina Sarolta, Veres Kata, Werner András. 4 pontot kapott: 28 versenyző. 3 pontot kapott: 14 versenyző. 2 pontot kapott: 17 versenyző. 1 pontot kapott: 15 versenyző. 0 pontot kapott: 20 versenyző.
A KöMaL 2017. októberi matematika feladatai

