 |
A C. 1439. feladat (2017. október) |
C. 1439. Milyen \(\displaystyle c\) érték esetén lesz az
\(\displaystyle {(x-5)}^2+ {(y-1)}^2 =c,\)
\(\displaystyle {(x-1)}^2+ {(y-5)}^2 =c\)
egyenletrendszernek egyetlen megoldása?
(5 pont)
A beküldési határidő 2017. november 10-én LEJÁRT.
1. megoldás. Az egyenletek bal oldalán négyzetszámok összege áll, így biztosan állíthatjuk, hogy \(\displaystyle c≥0\). Ezért tekinthetjük az egyenleteket derékszögű koordináta rendszerben lévő körök egyenleteinek. Az első az \(\displaystyle A(5;1)\) középpontú, \(\displaystyle r=\sqrt c\) sugarú, a másik a \(\displaystyle B(1;5)\) középpontú, \(\displaystyle r=\sqrt c\) sugarú kör egyenlete. Az egyenletrendszernek pontosan akkor van egy megoldása, ha a körök érintik egymást. Ekkor a középpontjaik távolsága éppen két sugárnyi távolság: \(\displaystyle AB=2r=2\sqrt c\).
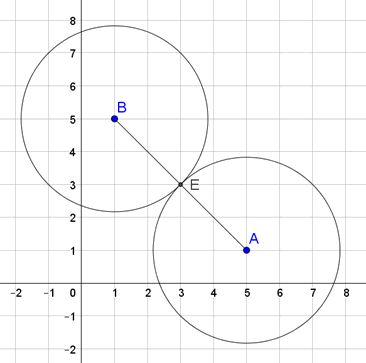
\(\displaystyle |\overrightarrow{AB}|=\sqrt{(1-5)^2+(5-1)^2}=\sqrt{32}=\sqrt{4c}.\)
Tehát \(\displaystyle c=8\) esetén van egy megoldás.
2. megoldás. Ha \(\displaystyle a\neq b\) és \(\displaystyle x=a\), \(\displaystyle y=b\) megoldás, akkor \(\displaystyle x=b\), \(\displaystyle y=a\) egy ettől különböző megoldás. Tehát ez nem lehetséges, így a megoldásban \(\displaystyle x=y\) lesz. Ekkor a két egyenlet megegyezik:
\(\displaystyle (x-5)^2+(x-1)^2=c,\)
\(\displaystyle 2x^2-12x+(26-c)=0.\)
Ennek akkor lesz egy megoldása, ha a diszkrimináns 0:
\(\displaystyle 12^2-8(26-c)=-64+8c=0,\)
amiből \(\displaystyle c=8\). Ebben az esetben lesz egy megoldása az egyenletrendszernek.
Statisztika:
139 dolgozat érkezett. 5 pontot kapott: 61 versenyző. 4 pontot kapott: 41 versenyző. 3 pontot kapott: 12 versenyző. 2 pontot kapott: 11 versenyző. 1 pontot kapott: 4 versenyző. 0 pontot kapott: 6 versenyző. Nem versenyszerű: 4 dolgozat.
A KöMaL 2017. októberi matematika feladatai

