Problem C. 1441. (November 2017)

C. 1441. A coffee shop serves coffee specials made from various ingredients. For any item selected from the menu there exist exactly three others that each have some ingredient in common with the selected item. If two menu items have no ingredient in common then there exists a third one that has an ingredient in common with each of the two. What is the maximum possible number of items on the menu of cofee specials?

(5 pont)

Deadline expired on December 11, 2017.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Legyenek az itallapon szereplő kávék egy egyszerű gráf csúcspontjai. Ha két kávénak van közös alapanyaga, akkor az ezeknek megfelelő csúcsokat kössük össze egy éllel. Az első feltétel pontosan azt jelenti, hogy a gráf minden csúcsának 3 a fokszáma, tehát minden csúcsból 3 él indul.

A második feltétel azt mondja ki, hogy ha két csúcsot nem köt össze él, akkor van olyan csúcs, amivel mindkettő össze van kötve. Ez pontosan azt jelenti, hogy bármely csúcsból bármely másik csúcsba legfeljebb két élen keresztül eljuthatunk.

Legyen a gráf egyik csúcsa \(\displaystyle A\), melyből egy-egy él vezet a \(\displaystyle B\), \(\displaystyle C\), \(\displaystyle D\) csúcsokba. Minden további \(\displaystyle X\) csúcsból kell vezetnie élnek a \(\displaystyle B\), \(\displaystyle C\) vagy \(\displaystyle D\) pontok valamelyikébe, különben az \(\displaystyle A\) és \(\displaystyle X\) csúcsokra nem teljesül a második feltétel.

A \(\displaystyle B\), \(\displaystyle C\), \(\displaystyle D\) csúcsokból \(\displaystyle A\)-n kívül még 2-2 csúcsba vezethet él, tehát az eddigi 4 csúcson kívül még legfeljebb \(\displaystyle 3\cdot2=6\) csúcsa lehet a gráfnak.

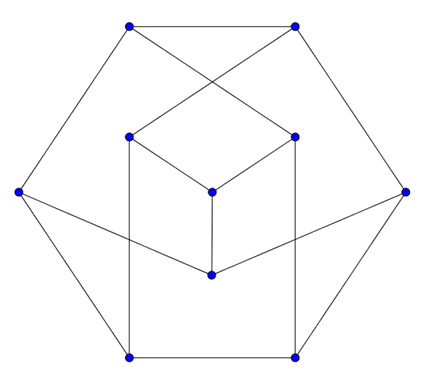
Ilyen 10 csúcsú gráf létezik (lásd az ábrát). Így legfeljebb 10 kávékülönlegesség lehet az itallapon.

Statistics:

89 students sent a solution.
5 points:	Ács Imre, Biró 424 Ádám, Czett Mátyás, Hámori Janka, Jánosdeák Márk, Kerekes Boldizsár, Koleszár Domonkos, Kovács 124 Kinga, Markó Gábor, Pinke Andrea, Shuborno Das, Sike 912 András, Szalontai Kinga Sára, Werner András, Williams Hajna.
4 points:	Bottlik Domonkos, Fonyi Máté Sándor, Forczek Bianka, Forgács Kata, Szente Péter.
3 points:	8 students.
2 points:	19 students.
1 point:	22 students.
0 point:	19 students.
Unfair, not evaluated:	1 solutions.

Problems in Mathematics of KöMaL, November 2017