 |
A C. 1442. feladat (2017. november) |
C. 1442. Egy háromszög \(\displaystyle a\), \(\displaystyle b\) és \(\displaystyle c\) oldalaira teljesül a következő összefüggés:
\(\displaystyle 1=\frac{1}{ab}+\frac{1}{bc}+\frac{1}{ac}. \)
Igazoljuk, hogy ekkor \(\displaystyle r\cdot R=\frac 12\), ahol \(\displaystyle r\) a háromszög beírható, \(\displaystyle R\) pedig a köré írható körének sugara.
Javasolta: Tatár Zsuzsanna Mária (Felsőgöd)
(5 pont)
A beküldési határidő 2017. december 11-én LEJÁRT.
Megoldás. Az adott összefüggést jobb oldalon közös nevezőre hozva és átrendezve:
\(\displaystyle 1=\frac{c+a+b}{abc},\)
\(\displaystyle abc=a+b+c.\)
Használjuk az 1. ábra jelöléseit. Az \(\displaystyle AFO\) derékszögű háromszögben \(\displaystyle \frac c2=R\cdot\sin γ\), vagyis \(\displaystyle \sin γ=\frac{c}{2R}\). Ezt behelyettesítve a háromszög területképletébe:
\(\displaystyle T=\frac{ab\cdot\sin γ}{2}=\frac{abc}{4R}.\)
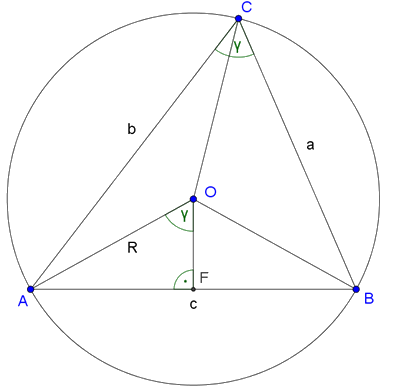
1. ábra
A háromszög beírt körének középpontját a csúcsokkal összekötve három részháromszöget kapunk (2. ábra). Ezek területének összege a háromszög területe:
\(\displaystyle T=\frac{ar}{2}+\frac{br}{2}+\frac{cr}{2}=\frac{r(a+b+c)}{2}.\)
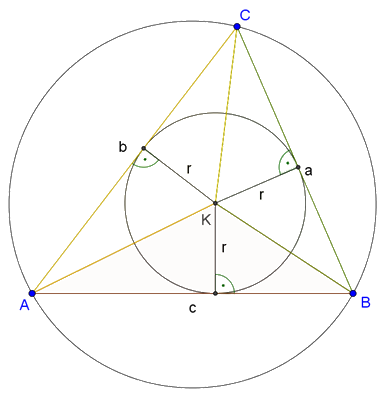
2. ábra
A két területképletből:
\(\displaystyle \frac{abc}{4R}=\frac{r(a+b+c)}{2}.\)
Felhasználva az adott összefüggésből kapott egyenlőséget leoszthatunk \(\displaystyle abc=a+b+c\neq0\)-val: \(\displaystyle \frac{1}{4R}=\frac r2\), vagyis \(\displaystyle rR=\frac12\).
Statisztika:
127 dolgozat érkezett. 5 pontot kapott: 118 versenyző. 4 pontot kapott: 1 versenyző. 3 pontot kapott: 3 versenyző. 1 pontot kapott: 1 versenyző. 0 pontot kapott: 4 versenyző.
A KöMaL 2017. novemberi matematika feladatai

