 Problem C. 1445. (November 2017)
Problem C. 1445. (November 2017)
C. 1445. The movie ``The Englishman Who Went up a Hill but Came down a Mountain'' is set in a Welsh village where the neighbouring mountain was designated as a hill by cartographers measuring its height. The villagers were too proud of their mountain to accept this. So they decided to raise its height from 984 feet to 1004 feet. They would carry earth onto the the hilltop shaped like a hemisphere of radius 82 feet, to build a truncated cone with its side tangent to the hemisphere and forming a \(\displaystyle 45^\circ\) angle with the horizontal (see the figure). Thus the height will exceed 1000 feet and the hill would qualify to be called a mountain. How many cubic feet of earth need to be carried onto the hilltop?
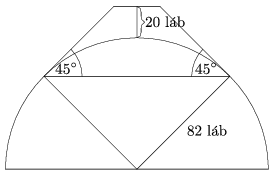
(5 pont)
Deadline expired on December 11, 2017.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Használjuk az ábra jelöléseit.
A hiányzó föld térfogata egy csonkakúp és egy gömbszelet térfogatának különbsége.
A csonkakúp síkmetszete az ábrán az \(\displaystyle ABCD\) trapéz, a gömbszeleté pedig az \(\displaystyle ABG\) körszelet. A mértékegység a hosszúságoknál mindenütt láb.
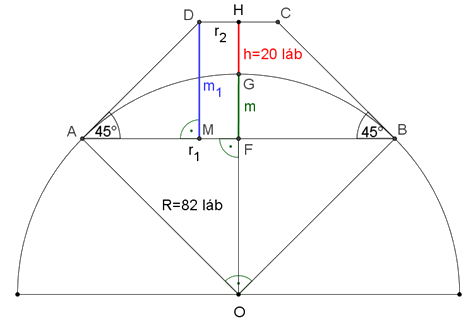
Mivel \(\displaystyle AD\) érintő, ezért \(\displaystyle DAO\angle=90^{\circ}\) és így \(\displaystyle FAO\angle=45^{\circ}\). Tehát az \(\displaystyle AFO\) egyenlő szárú derékszögű háromszög, ezért \(\displaystyle FO=FA=\frac{R}{\sqrt2}=\frac{82}{\sqrt2}=41\sqrt2\).
A gömbszelet magassága \(\displaystyle m=R-FO=82-41\sqrt2≈24,017\), sugara \(\displaystyle r_1=FA=41\sqrt2≈57,983\).
A gömbszelet térfogata: \(\displaystyle V_{gsz}=\frac{πm(3r_1^2+m^2)}{6}≈134088,9\).
A csonkakúp alapkörének sugara szintén \(\displaystyle r_1≈57,983\), magassága \(\displaystyle m_1=m+h=82-41\sqrt2+20=102-41\sqrt2≈44,017\).
Az \(\displaystyle ADM\) egyenlő szárú derékszögű háromszög, ezért \(\displaystyle AM=DM= m_1\).
A csonkakúp fedőkörének sugara \(\displaystyle r_2=DH=MF=AF-AM=r_1-m_1≈13,966\).
A csonkakúp térfogata: \(\displaystyle V_{cs}=\frac{πm_1(r_1^2+r_1 r_2+r_2^2)}{3}≈201288,6\).
A szükséges föld térfogata: \(\displaystyle V_F=V_{cs}-V_{gsz}≈67200\) köbláb.
Statistics:
166 students sent a solution. 5 points: 65 students. 4 points: 42 students. 3 points: 24 students. 2 points: 18 students. 1 point: 5 students. 0 point: 3 students. Unfair, not evaluated: 9 solutionss.
Problems in Mathematics of KöMaL, November 2017
