A C. 1446. feladat (2017. november)

C. 1446. Az \(\displaystyle ABCD\) paralelogramma belsejében vegyük fel a \(\displaystyle Q\) pontot úgy, hogy \(\displaystyle AQB\sphericalangle+CQD\sphericalangle=180^{\circ}\) legyen. Bizonyítsuk be, hogy \(\displaystyle QBA\sphericalangle=QDA\sphericalangle\) és \(\displaystyle QAD\sphericalangle=QCD\sphericalangle\).

(5 pont)

A beküldési határidő 2017. december 11-én LEJÁRT.

Megoldás. Használjuk az ábra jelöléseit: legyen \(\displaystyle AQB∡=ε\), \(\displaystyle QBA∡=β\) és \(\displaystyle QCD∡=α\).

Mivel \(\displaystyle ABCD\) paralelogramma, ezért \(\displaystyle \overrightarrow{AD}=\overrightarrow{BC}\). Toljuk el az \(\displaystyle AQB\) háromszöget ezzel a vektorral, ekkor az \(\displaystyle AB\) szakasz a \(\displaystyle DC\) szakaszba kerül, a \(\displaystyle Q\) pont képét pedig jelölje \(\displaystyle P\). Az így kapott \(\displaystyle AQB\) háromszög egybevágó a \(\displaystyle DPC\) háromszöggel, így megfelelő szögeik egyenlőek: \(\displaystyle ABQ∡=DCP∡=β\) és \(\displaystyle AQB∡=DPC∡=ε\).

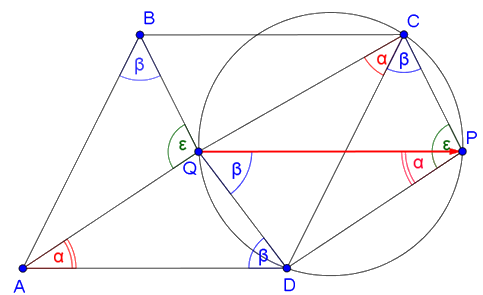
Mivel a feltétel szerint \(\displaystyle AQB∡+CQD∡=180°\), ezért az eltolás miatt \(\displaystyle DPC∡+CQD∡=180°\) is igaz. Ez azt jelenti, hogy a \(\displaystyle DPCQ\) négyszög húrnégyszög. Felhasználva a körülírt körben az azonos íven nyugvó kerületi szögek egyenlőségét: \(\displaystyle QCD∡=QPD∡=α\) és \(\displaystyle PCD∡=PQD∡=β\).

Az eltolás miatt \(\displaystyle \overrightarrow{AQ}=\overrightarrow{DP}\), az \(\displaystyle ADPQ\) négyszög paralelogramma, így \(\displaystyle QPD∡=QAD∡=α\), mert szemközti szögek, \(\displaystyle DQP∡=QDA∡=β\), mert váltószögek.

Összefoglalva: \(\displaystyle QBA∡=β=QDA∡\) és \(\displaystyle QAD∡=α=QCD∡\). Ezt kellett bizonyítanunk.

Statisztika:

36 dolgozat érkezett.
5 pontot kapott:	Agócs Katinka, Ajtai Boglárka, Bukor Benedek, Debreczeni Tibor, Gárdonyi Csilla Dóra, Herpai Ádám, Horváth 31 László, Jankovits András, Kovács 161 Márton Soma, Mészáros 916 Márton, Molnár 410 István, Németh Csilla Márta, Paksi Barnabás, Sal Dávid, Spányik Teodor, Surján Anett, Szécsi Adél Lilla, Varga-Molnár Bertalan.
4 pontot kapott:	Almási Adél Csilla, Wolff Vilmos.
3 pontot kapott:	1 versenyző.
2 pontot kapott:	6 versenyző.
1 pontot kapott:	5 versenyző.
0 pontot kapott:	4 versenyző.

A KöMaL 2017. novemberi matematika feladatai