Problem C. 1451. (December 2017)

C. 1451. Where does the curve of equation \(\displaystyle y=x|x|-2x+3\) intersect the \(\displaystyle x\) axis? Find the location and type of local extrema of this curve, and determine the corresponding \(\displaystyle y\) coordinates.

(5 pont)

Deadline expired on January 10, 2018.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Bontsuk két részre az \(\displaystyle y=x|x|-2x+3\) függvényt az \(\displaystyle x\) előjelétől függően:

Ha \(\displaystyle x≥0\), akkor \(\displaystyle |x|=x\) és \(\displaystyle y=x^2-2x+3=(x-1)^2+2\).

Ha \(\displaystyle x<0\), akkor \(\displaystyle |x|=-x\) és \(\displaystyle y=-x^2-2x+3=-(x+1)^2+4\).

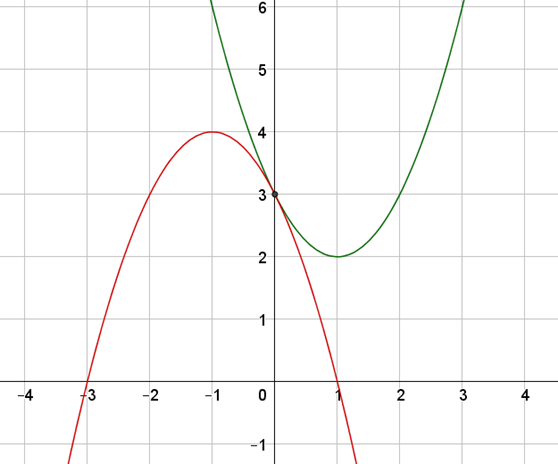
\(\displaystyle x≥0\) esetén a függvény nem metszi az \(\displaystyle x\) tengelyt, mivel \(\displaystyle (x-1)^2+2>0\).

\(\displaystyle x<0\) esetén \(\displaystyle -(x+1)^2+4=0\) negatív megoldása \(\displaystyle x=-3\), ez a zérushely.

\(\displaystyle x≥0\) esetén az \(\displaystyle y=(x-1)^2+2\) függvénynek akkor van minimuma, ha \(\displaystyle x-1=0\), tehát a lokális minimum helye \(\displaystyle x=1\), értéke \(\displaystyle y=2\).

\(\displaystyle x<0\) esetén az \(\displaystyle y=-(x+1)^2+4\) függvénynek akkor van maximuma, ha \(\displaystyle x+1=0\), tehát a lokális maximum helye \(\displaystyle x=-1\), értéke \(\displaystyle y=4\).

Statistics:

225 students sent a solution.
5 points:	114 students.
4 points:	43 students.
3 points:	15 students.
2 points:	29 students.
1 point:	13 students.
0 point:	7 students.
Unfair, not evaluated:	4 solutionss.

Problems in Mathematics of KöMaL, December 2017