 |
A C. 1452. feladat (2017. december) |
C. 1452. Egy 13 cm sugarú körbe írható trapézról tudjuk, hogy átlói a kör középpontjától 5 cm-re helyezkednek el. Legfeljebb mekkora lehet a trapéz területe?
(5 pont)
A beküldési határidő 2018. január 10-én LEJÁRT.
Megoldás. Használjuk az ábra jelöléseit. A kör sugara \(\displaystyle r=13\) cm, az átlók távolsága a kör középpontjától \(\displaystyle OF=OG=d=5\) cm.
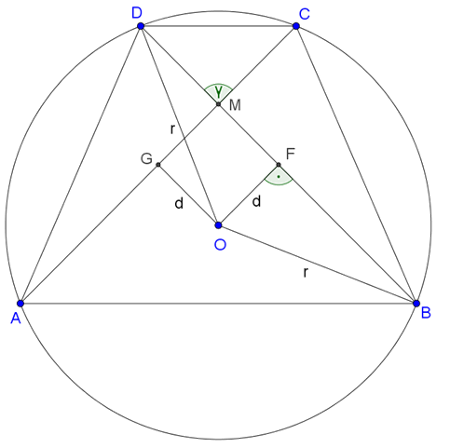
A trapéz átlói a körben húrok. A húr felező merőlegese átmegy a középponton. Legyen a \(\displaystyle BD\) átló felezőpontja az \(\displaystyle F\) pont. A Pitagorasz-tételt használva a \(\displaystyle BFO\) derékszögű háromszögben:
\(\displaystyle BF=\sqrt{r^2-d^2}=\sqrt{13^2-5^2}=\sqrt{144}=12 \mathrm{~cm}.\)
\(\displaystyle AC= BD=2BF=24 \mathrm{~cm}.\)
A trapéz területe:
\(\displaystyle T=\frac12\cdot AC\cdot BD\cdot \sinγ=\frac 12\cdot 24\cdot24\cdot\sinγ=288\cdot\sinγ.\)
Ez akkor maximális, ha \(\displaystyle \sinγ=1\), vagyis \(\displaystyle γ=90°\). Ekkor \(\displaystyle T_{max}=288 \mathrm{~cm}^2\).
Statisztika:
102 dolgozat érkezett. 5 pontot kapott: 63 versenyző. 4 pontot kapott: 1 versenyző. 3 pontot kapott: 10 versenyző. 2 pontot kapott: 12 versenyző. 1 pontot kapott: 6 versenyző. 0 pontot kapott: 6 versenyző. Nem versenyszerű: 4 dolgozat.
A KöMaL 2017. decemberi matematika feladatai

