 |
A C. 1454. feladat (2017. december) |
C. 1454. Egy szálloda recepcióján egymás mellé került London és Moszkva külsejében egyforma órája. Egy pók hálóját a két óra kismutatója közé feszítette ki, majd helyet foglalt rajta úgy, hogy a rugalmasan megnyúló szál által képzett szakasznak mindvégig a felezőpontjában tartózkodott. Milyen pályát ír le a pók 24 óra alatt? (London és Moszkva között az időeltolódás 3 óra.)
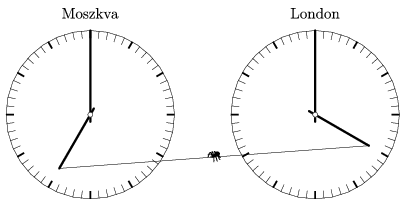
(5 pont)
A beküldési határidő 2018. január 10-én LEJÁRT.
Megoldás. Szemléltessük az óramutatók pályáját a derékszögű koordináta rendszerben az \(\displaystyle O_L (1+p;0)\) és az \(\displaystyle O_M (-1-p;0)\) középpontú egység sugarú körökkel (vagyis legyen a koordinátarendszerben az egység éppen az órák sugara).

Az időeltolódás miatt egyik mutató az \(\displaystyle L_1\), másik az \(\displaystyle M_1\) pontból indul. Legyenek a mutatók \(\displaystyle t\) idő elteltével az \(\displaystyle L\) és \(\displaystyle M\) pontokban.
Legyen \(\displaystyle LO_L L_1∡=MO_M M_1∡=α=ωt\), ahol \(\displaystyle ω\) a kismutatók szögsebessége.
Ekkor az \(\displaystyle L\) pont koordinátái \(\displaystyle x_L=1+p+\cosα\) és \(\displaystyle y_L=-\sinα\); az \(\displaystyle R\) pont koordinátái pedig \(\displaystyle x_M=-1-p-\sinα\) és \(\displaystyle y_M=-\cosα\).
A pók helyzetének, vagyis az \(\displaystyle LM\) szakasz felezőpontjának koordinátái: \(\displaystyle x_F=\frac{\cosα-\sinα}{2}\), \(\displaystyle y_F=\frac{-\sinα-\cosα}{2}\).
\(\displaystyle x_F^2+y_F^2=\frac{\cos^2 α-2\cosα\cdot\sinα+\sin^2 α}{4}+\frac{\cos^2 α+2\cosα\cdot\sinα+\sin^2 α}{4}=\)
\(\displaystyle =\frac{2(\cos^2 α+\sin^2 α)}{4}=\frac12.\)
Ez egy origó középpontú kör egyenlete, melynek sugara \(\displaystyle r=\frac{\sqrt2}{2}\).
Tehát a pók körpályán mozog, és 24 óra alatt kétszer is végigmegy rajta.
Statisztika:
55 dolgozat érkezett. 5 pontot kapott: Ajtai Boglárka, Balog 518 Lóránd, Bukor Benedek, Debreczeni Tibor, Jankovits András, Kiszelovics Dorina, Molnár 410 István, Németh Csilla Márta, Nyitrai Boglárka, Sal Dávid, Szécsi Adél Lilla. 4 pontot kapott: Agócs Katinka, Lénárd Kristóf, Magyar 257 Boglárka, Mészáros 916 Márton, Négyessy Eszter, Paksi Barnabás, Rittgasszer Ákos, Surján Anett, Szőnyi Laura, Varga Dániel Jonatán, Vlaszov Artúr, Wolff Vilmos. 3 pontot kapott: 6 versenyző. 2 pontot kapott: 4 versenyző. 1 pontot kapott: 18 versenyző. 0 pontot kapott: 4 versenyző.
A KöMaL 2017. decemberi matematika feladatai

