 Problem C. 1454. (December 2017)
Problem C. 1454. (December 2017)
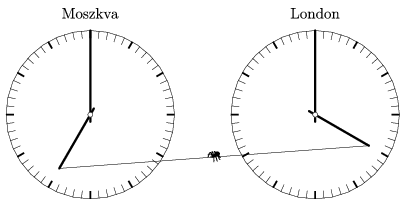
C. 1454. There are two identical clocks at the reception of a hotel. One clock shows the time in London, and the other shows the time in Moscow. A spider has made a web between the hour hands of the two clocks. While the thread is stretching elastically, the spider always stays at the midpoint. What will be the path described by the spider during the course of 24 hours? (The time lag between London and Moscow is 3 hours.)
(5 pont)
Deadline expired on January 10, 2018.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Szemléltessük az óramutatók pályáját a derékszögű koordináta rendszerben az \(\displaystyle O_L (1+p;0)\) és az \(\displaystyle O_M (-1-p;0)\) középpontú egység sugarú körökkel (vagyis legyen a koordinátarendszerben az egység éppen az órák sugara).

Az időeltolódás miatt egyik mutató az \(\displaystyle L_1\), másik az \(\displaystyle M_1\) pontból indul. Legyenek a mutatók \(\displaystyle t\) idő elteltével az \(\displaystyle L\) és \(\displaystyle M\) pontokban.
Legyen \(\displaystyle LO_L L_1∡=MO_M M_1∡=α=ωt\), ahol \(\displaystyle ω\) a kismutatók szögsebessége.
Ekkor az \(\displaystyle L\) pont koordinátái \(\displaystyle x_L=1+p+\cosα\) és \(\displaystyle y_L=-\sinα\); az \(\displaystyle R\) pont koordinátái pedig \(\displaystyle x_M=-1-p-\sinα\) és \(\displaystyle y_M=-\cosα\).
A pók helyzetének, vagyis az \(\displaystyle LM\) szakasz felezőpontjának koordinátái: \(\displaystyle x_F=\frac{\cosα-\sinα}{2}\), \(\displaystyle y_F=\frac{-\sinα-\cosα}{2}\).
\(\displaystyle x_F^2+y_F^2=\frac{\cos^2 α-2\cosα\cdot\sinα+\sin^2 α}{4}+\frac{\cos^2 α+2\cosα\cdot\sinα+\sin^2 α}{4}=\)
\(\displaystyle =\frac{2(\cos^2 α+\sin^2 α)}{4}=\frac12.\)
Ez egy origó középpontú kör egyenlete, melynek sugara \(\displaystyle r=\frac{\sqrt2}{2}\).
Tehát a pók körpályán mozog, és 24 óra alatt kétszer is végigmegy rajta.
Statistics:
55 students sent a solution. 5 points: Ajtai Boglárka, Balog 518 Lóránd, Bukor Benedek, Debreczeni Tibor, Jankovits András, Kiszelovics Dorina, Molnár 410 István, Németh Csilla Márta, Nyitrai Boglárka, Sal Dávid, Szécsi Adél Lilla. 4 points: Agócs Katinka, Lénárd Kristóf, Magyar 257 Boglárka, Mészáros 916 Márton, Négyessy Eszter, Paksi Barnabás, Rittgasszer Ákos, Surján Anett, Szőnyi Laura, Varga Dániel Jonatán, Vlaszov Artúr, Wolff Vilmos. 3 points: 6 students. 2 points: 4 students. 1 point: 18 students. 0 point: 4 students.
Problems in Mathematics of KöMaL, December 2017
