Problem C. 1457. (January 2018)

C. 1457. An isosceles right-angled triangle inscribed in a circle is rotated through 45 degrees about the centre of the circle. Find the perimeter and area of the intersection of the two triangles.

(5 pont)

Deadline expired on February 12, 2018.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Használjuk az ábra jelöléseit. Ha a sugár egységnyi, akkor \(\displaystyle AB=2r=2\).

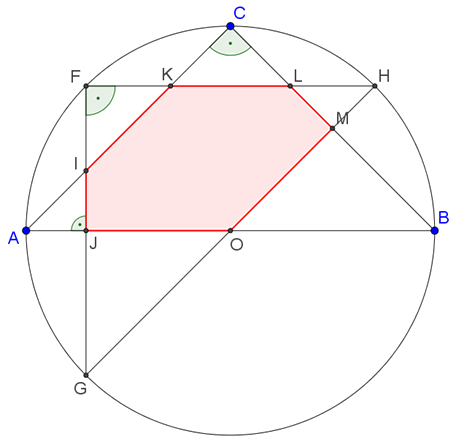
Az \(\displaystyle ABC\) és \(\displaystyle FGH\) egyenlő szárú derékszögű háromszögek befogóinak hossza:

\(\displaystyle AC=BC=FG=FH=\frac{2}{\sqrt2}=\sqrt2.\)

A \(\displaystyle 45°\)-os elforgatás miatt az \(\displaystyle AB\) átmérő merőleges a \(\displaystyle GF\) húrra és felezi azt, hasonlóan a \(\displaystyle GH\) átmérő felezi a \(\displaystyle BC\) húrt, ezért \(\displaystyle FJ=GJ=BM=CM=\frac{\sqrt2}{2}\).

\(\displaystyle GJO\) és \(\displaystyle BMO\) is egyenlő szárú derékszögű háromszögek, átfogójuk a kör sugara, tehát \(\displaystyle 1\). Befogóik: \(\displaystyle GJ=OJ=BM=MO=\frac{\sqrt2}{2}\).

\(\displaystyle AJ=AO-OJ=1-\frac{\sqrt2}{2}=\frac{2-\sqrt2}{2}.\)

\(\displaystyle AJI\) és \(\displaystyle HML\) egybevágó egyenlő szárú derékszögű háromszögek. Befogóik: \(\displaystyle AJ=JI=HM=ML=1-\frac{\sqrt2}{2}=\frac{2-\sqrt2}{2}.\)

\(\displaystyle FI=FJ-JI=\frac{\sqrt2}{2}-\left(1-\frac{\sqrt2}{2}\right)=\sqrt2-1.\)

\(\displaystyle FIK\) és \(\displaystyle CKL\) egybevágó egyenlő szárú derékszögű háromszögek. Befogóik: \(\displaystyle FI=FK=CK=CL=\sqrt2-1\). Átfogóik: \(\displaystyle KL=IK=\sqrt2\cdot FI=2-\sqrt2\).

A keresett kerület:

\(\displaystyle K_k=OJ+JI+IK+KL+LM+MO=2\cdot OJ+2\cdot JI+2\cdot IK=\)

\(\displaystyle 2\cdot\frac{\sqrt2}{2}+2\cdot\frac{2-\sqrt2}{2}+2\cdot(2-\sqrt2)=\sqrt2+2-\sqrt2+4-2\sqrt2=6-2\sqrt2≈3,1716.\)

A keresett terület:

\(\displaystyle T_k=T_{ABC}-T_{BMO}-T_{CKL}-T_{AIJ}=\frac{\sqrt2^2}{2}-\frac12\cdot\left(\frac{\sqrt2}{2}\right)^2-\frac12\cdot(\sqrt2-1)^2-\frac12\cdot\left(\frac{2-\sqrt2}{2}\right)^2=\)

\(\displaystyle =1-\frac14-\frac32+\frac{2\sqrt2}{2}-\frac34+\frac{\sqrt2}{2}=\frac{3\sqrt2}{2}-\frac32=\frac{3\cdot(\sqrt2-1)}{2}≈0,6213.\)

Statistics:

165 students sent a solution.
5 points:	70 students.
4 points:	27 students.
3 points:	21 students.
2 points:	13 students.
1 point:	15 students.
0 point:	19 students.

Problems in Mathematics of KöMaL, January 2018