Problem C. 1459. (January 2018)

C. 1459. Reflect the parabola \(\displaystyle y=x^2\) about the point \(\displaystyle F\left(0,\frac 14\right)\). At what angle do the two parabolas intersect?

(5 pont)

Deadline expired on February 12, 2018.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Az \(\displaystyle y=x^2\) parabolát a \(\displaystyle \left(0;\frac14\right)\) pontra tükrözve az \(\displaystyle y=-x^2+\frac12\) parabolát kapjuk.

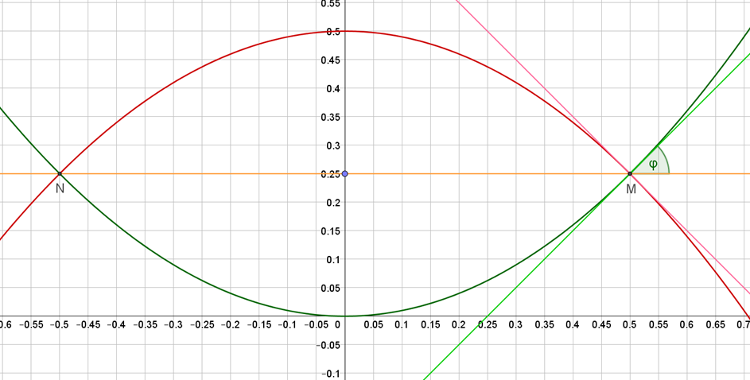
A metszéspontok \(\displaystyle x\) koordinátáit az \(\displaystyle x^2=-x^2+\frac12\) egyenletből kapjuk. Rendezve: \(\displaystyle x^2=\frac14\), amiből \(\displaystyle x_1=\frac12\), \(\displaystyle x_2=-\frac12\). Így a metszéspontok koordinátái: \(\displaystyle M\left(\frac12;\frac14\right)\) és \(\displaystyle N\left(-\frac12;\frac14\right)\).

Ha meghatározzuk az \(\displaystyle M\) pontban az \(\displaystyle y=x^2\) parabola érintőjének \(\displaystyle φ\) irányszögét, akkor a szimmetria miatt az érintők által bezárt szög az \(\displaystyle M\) és \(\displaystyle N\) pontban is \(\displaystyle 2φ\) lesz.

Legyen a keresett érintő egyenlete: \(\displaystyle y=mx+b\). Mivel átmegy az \(\displaystyle M\left(\frac12;\frac14\right)\) ponton, ezért egyenlete \(\displaystyle \frac14=\frac12 m+b\), amiből \(\displaystyle b=-\frac12 m+\frac14\). Ezt visszahelyettesítve:

\(\displaystyle y=mx-\frac12 m+\frac14.\)

Ha ez érintője az \(\displaystyle y=x^2\) parabolának, akkor az \(\displaystyle x^2=mx-\frac12 m+\frac14\) másodfokú egyenletnek csak egy megoldása van. Rendezve: \(\displaystyle x^2- mx+\frac12 m-\frac14=0\). Pontosan akkor van egy megoldása, ha a diszkrimináns értéke nulla: \(\displaystyle D=m^2-2m+1=0\), vagyis \(\displaystyle (m-1)^2=0\). Tehát az érintő meredeksége \(\displaystyle m=1\).

\(\displaystyle \tgφ=1\), vagyis az irányszög \(\displaystyle φ=45°\). Az érintők által, vagyis a két parabola által bezárt szög \(\displaystyle 2φ=90°\).

Statistics:

126 students sent a solution.
5 points:	62 students.
4 points:	11 students.
3 points:	7 students.
2 points:	7 students.
1 point:	7 students.
0 point:	32 students.

Problems in Mathematics of KöMaL, January 2018