 |
A C. 1463. feladat (2018. február) |
C. 1463. A szabályos \(\displaystyle ABC\) háromszög belsejében található \(\displaystyle M\) pontból az \(\displaystyle AB\), \(\displaystyle BC\) és \(\displaystyle CA\) oldalakra állított merőlegesek talppontja rendre \(\displaystyle H\), \(\displaystyle K\) és \(\displaystyle P\). Bizonyítsuk be, hogy
\(\displaystyle (i)\) \(\displaystyle {|AH|}^2+{|BK|}^2+{|CP|}^2= {|HB|}^2+{|KC|}^2+{|PA|}^2\);
\(\displaystyle (ii)\) \(\displaystyle |AH|+|BK|+|CP|= |HB|+|KC|+|PA|\).
Mathematical Competitions in Croatia
(5 pont)
A beküldési határidő 2018. március 12-én LEJÁRT.
Megoldás. \(\displaystyle (i)\) Használjuk az 1. ábra jelöléseit.
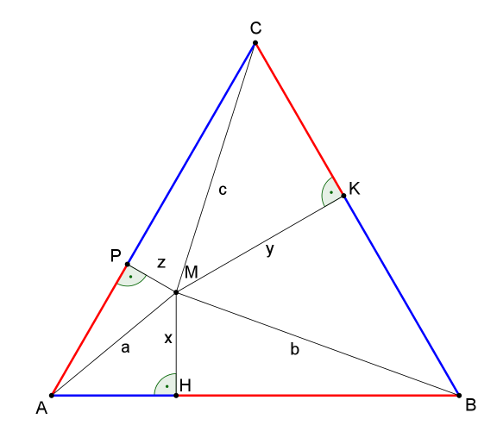
1. ábra
Írjuk fel a Pitagorasz-tételt a derékszögű részháromszögekre:
\(\displaystyle a^2=|AH|^2+x^2,\)
\(\displaystyle a^2=|PA|^2+z^2,\)
\(\displaystyle b^2=|HB|^2+x^2,\)
\(\displaystyle b^2=|BK|^2+y^2,\)
\(\displaystyle c^2=|KC|^2+y^2,\)
\(\displaystyle c^2=|CP|^2+z^2.\)
Ebből a kék szakaszokra: \(\displaystyle a^2+b^2+c^2=|AH|^2+x^2+|BK|^2+y^2 +|CP|^2+z^2\).
A piros szakaszokra: \(\displaystyle a^2+b^2+c^2=|HB|^2+x^2+|KC|^2+y^2+|PA|^2+z^2\).
Ebből \(\displaystyle |AH|^2+x^2+|BK|^2+y^2 +|CP|^2+z^2=|HB|^2+x^2+|KC|^2+y^2+|PA|^2+z^2\), vagyis \(\displaystyle |AH|^2+|BK|^2+|CP|^2=|HB|^2+|KC|^2+|PA|^2\).
\(\displaystyle (ii)\) Legyenek az \(\displaystyle M\) ponton áthaladó \(\displaystyle A_1B_2\), \(\displaystyle B_1C_2\) és \(\displaystyle C_1A_2\) szakaszok párhuzamosak a megfelelő oldalakkal a 2. ábra szerint.
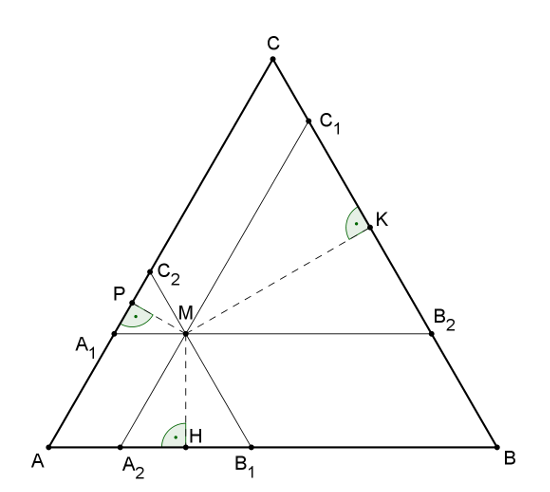
2. ábra
\(\displaystyle MH\), \(\displaystyle MK\) és \(\displaystyle MP\) rendre a \(\displaystyle B_1MA_2\), \(\displaystyle C_1MB_2\) és \(\displaystyle A_1MC_2\) szabályos háromszögek súlyvonalai, továbbá \(\displaystyle |AA_1|=|A_2M|=|B_1M|=|BB_2|\), \(\displaystyle |BB_1|=|B_2M|=|C_1M|=|CC_2|\) és \(\displaystyle |CC_1|=|C_2M|=|A_1M|=|AA_2|\). Mindebből kapjuk, hogy
\(\displaystyle |AH|+|BK|+|CP|=|AA_2|+|A_2H|+|BB_2|+|B_2K|+|CC_2|+|C_2P|=\)
\(\displaystyle =|C_1C|+|HB_1|+|A_1A|+|KC_1|+|B_1B|+|PA_1|=\)
\(\displaystyle =|HB_1|+|B_1B|+|KC_1|+|C_1C|+|PA_1|+|A_1A|=|HB|+|KC|+|PA|.\)
Statisztika:
74 dolgozat érkezett. 5 pontot kapott: Ács Imre, Al-Hag Máté Amin, Andó Viola, Bérczi Péter, Biró 424 Ádám, Csóti Balázs , Czett Mátyás, Debreczeni Dorina, Fonyi Máté Sándor, Forgács Kata, Gál Bence, Gém Viktória, Hámori Janka, Harmath Eszter, Hordós Adél Zita, Horváth Antal, Jánosdeák Márk, Kerekes Boldizsár, Kis 194 Károly, Kiss 014 Dávid, Kovács 157 Zita, Kovács Fruzsina Dóra, Kovács-Deák Zsombor, Markó Gábor, Nagy 202 Eszter , Pinke Andrea, Rusvai Miklós, Shuborno Das, Szőke Péter, Urszuly Csenge, Veibli-Magyari Kristóf, Werner András. 4 pontot kapott: Ámmer Fanni, Dózsa Ferenc, Horváth 999 Anikó, Oláh Zsófia, Schenk Anna, Székelyhidi Klára. 3 pontot kapott: 30 versenyző. 2 pontot kapott: 1 versenyző. 1 pontot kapott: 3 versenyző. 0 pontot kapott: 2 versenyző.
A KöMaL 2018. februári matematika feladatai

