Problem C. 1465. (February 2018)

C. 1465. Let \(\displaystyle M\) denote the intersection of the lines \(\displaystyle PS\) and \(\displaystyle RT\) passing through the vertices of a regular triangle \(\displaystyle PQR\) and a square \(\displaystyle QRST\). Show that triangle \(\displaystyle PTM\) is isosceles.

(5 pont)

Deadline expired on March 12, 2018.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. 1. eset. A \(\displaystyle P\) pont a négyzeten kívül van. Használjuk az 1. ábra jelöléseit. A tengelyes szimmetria miatt \(\displaystyle PQT\) és \(\displaystyle PRS\) egyenlő szárú háromszögek egybevágóak.

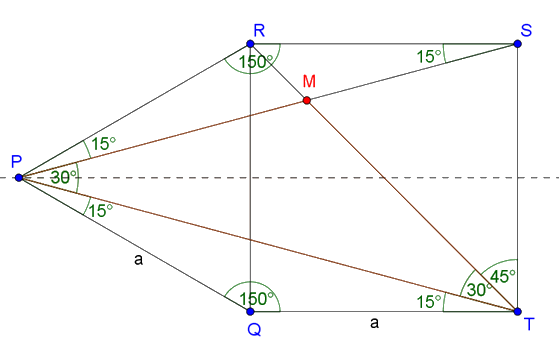
1. ábra

\(\displaystyle PQT∡=PRS∡=60°+90°=150°,\)

\(\displaystyle QPT∡+QTP∡=180°-150°=30°.\)

Ezért

\(\displaystyle QPT∡=QTP∡=RPS∡=15°.\)

Az \(\displaystyle RST\) egyenlő szárú derékszögű háromszögben \(\displaystyle RTS∡=45°\).

\(\displaystyle TPM∡=QPR∡-QPT∡-RPS∡=60°-15°-15°=30°,\)

\(\displaystyle PTM∡=QTS∡-QTP∡-RTS∡=90°-15°-45°=30°.\)

A \(\displaystyle PTM\) háromszögben \(\displaystyle PTM∡=TPM∡\), ezért a háromszög egyenlő szárú.

2. eset: A \(\displaystyle P\) pont a négyzet belsejében van. Használjuk a 2. ábra jelöléseit.

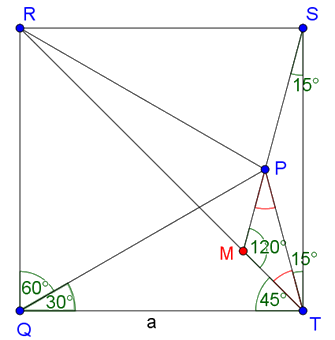
2. ábra

A \(\displaystyle PQR\) egyenlő oldalú háromszögben \(\displaystyle PQR∡=60°\). \(\displaystyle PQT∡=90°-PRQ∡=30°\).

A \(\displaystyle PQT\) egyenlő szárú háromszögben \(\displaystyle QTP∡=QPT∡=(180°-30°)/2=75°\).

A \(\displaystyle PST\) egyenlő szárú háromszögben \(\displaystyle PTS∡=PST∡=90°-75°=15°\).

A \(\displaystyle PTM\) háromszögben \(\displaystyle PTM∡=90°-45°-15°=30°\). Az \(\displaystyle SMT\) háromszögben \(\displaystyle SMT∡=180°-45°-15°=120°\). Ezért \(\displaystyle MPT∡=180°-120°-30°=30°\). Tehát az \(\displaystyle PTM\) háromszög egyenlő szárú.

Statistics:

180 students sent a solution.
5 points:	54 students.
4 points:	5 students.
3 points:	107 students.
2 points:	7 students.
1 point:	2 students.
0 point:	3 students.
Unfair, not evaluated:	2 solutionss.

Problems in Mathematics of KöMaL, February 2018