 Problem C. 1467. (February 2018)
Problem C. 1467. (February 2018)
C. 1467. Let \(\displaystyle A\) and \(\displaystyle B\) denote the intersection of the circle of radius \(\displaystyle 2r\) centred at \(\displaystyle O\), and the circle of radius \(\displaystyle r+1\) passing through \(\displaystyle O\). How long may \(\displaystyle r\) be if the line segment \(\displaystyle AB\) is the diameter of the smaller circle?
(5 pont)
Deadline expired on March 12, 2018.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Használjuk az ábra jelöléseit.
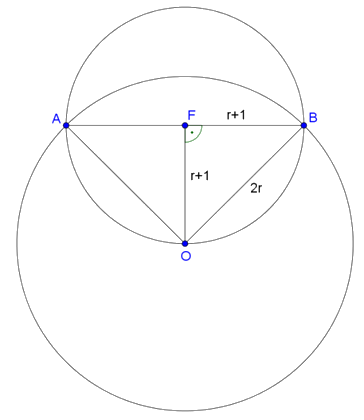
Az \(\displaystyle AB\) szakasz \(\displaystyle F\) felezőpontja a kisebb kör középpontja. Az \(\displaystyle FO\) egyenes a húr felező merőlegese. \(\displaystyle FO=FB=r+1\). Ezért \(\displaystyle BFO\) egyenlőszárú, derékszögű háromszög. Így az átfogó: \(\displaystyle BO=\sqrt2\cdot BF\).
A \(\displaystyle BO\) oldal a nagy kör sugara, ezért \(\displaystyle BO=2r\). Vagyis \(\displaystyle 2r=\sqrt2(r+1)\).
\(\displaystyle \sqrt2\)-vel leosztva: \(\displaystyle \sqrt2 r=r+1\).
Rendezve és gyöktelenítve a nevezőt: \(\displaystyle r=\frac{1}{\sqrt2-1}\cdot\frac{\sqrt2+1}{\sqrt2+1}=\sqrt2+1\).
Tehát \(\displaystyle r=\sqrt2+1\).
Statistics:
64 students sent a solution. 5 points: Agócs Katinka, Balog 518 Lóránd, Bodgál Attila Zoltán, Böcskei Bálint Attila, Bukor Benedek, Debreczeni Tibor, Dékány Barnabás, Dobay Ádám, Draskóczi Dóra Boglárka, Horváth 31 László, Jankovits András, Kiszelovics Dorina, Madarász Tamás, Magyar 257 Boglárka, Mészáros 916 Márton, Mészáros Melinda, Molnár 410 István, Molnár 921 Ádám, Németh Csilla Márta, Nyitrai Boglárka, Pszota Máté, Sal Dávid, Sándor Boglárka, Surján Anett, Szécsi Adél Lilla, Szűcs 865 Eszter, Varga 269 Viktor, Vezse Botond, Vlaszov Artúr. 4 points: Ajtai Boglárka, Almási Adél Csilla, Apró 936 Dániel, Deák Péter, Gere Virág, Gréczi Gergely Ádám, Kovács 111 Bence, Kovács 161 Márton Soma, Lapu Kolos, Lénárd Kristóf, Martos Letícia, Paksi Barnabás, Pipis Panna, Rittgasszer Ákos, Spányik Teodor, Szepessy Luca, Tóth Imre, Török Boldizsár, Varga Dániel Jonatán, Wolff Vilmos, Zentai Flóra. 3 points: 10 students. 2 points: 2 students. 0 point: 2 students.
Problems in Mathematics of KöMaL, February 2018
