 |
A C. 1469. feladat (2018. március) |
C. 1469. Az \(\displaystyle ABC\) háromszög \(\displaystyle C\) csúcsából induló magasság talppontja \(\displaystyle T\) (az \(\displaystyle AB\) oldal belső pontja), \(\displaystyle R\) pedig a szögfelezőé: \(\displaystyle AB=10\), \(\displaystyle AT=3\), \(\displaystyle AR=4\). Határozzuk meg a háromszög oldalainak a hosszát.
(5 pont)
A beküldési határidő 2018. április 10-én LEJÁRT.
Megoldás. Használjuk az ábra jelöléseit. \(\displaystyle AB=10\), \(\displaystyle AR=4\), \(\displaystyle AT=3\), ezért \(\displaystyle RB=6\), \(\displaystyle TR=1\) és \(\displaystyle TB=7\). A szögfelező a szemközti oldalt a szomszédos oldalak arányában metszi, ezért \(\displaystyle \frac ab=\frac64=\frac32\). Tehát \(\displaystyle a=\frac32 b\).
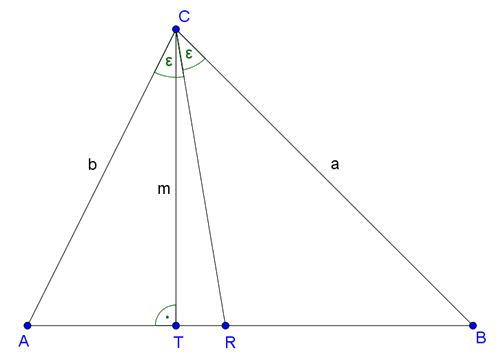
Írjuk fel a Pitagorasz-tételt az \(\displaystyle ATC\) és \(\displaystyle BTC\) derékszögű háromszögekre:
\(\displaystyle m^2+3^2=b^2,\)
\(\displaystyle m^2+7^2=a^2.\)
Vonjuk ki az alsó egyenletből a felsőt és helyettesítsünk be \(\displaystyle a\) helyére \(\displaystyle \frac32 b\)-t:
\(\displaystyle 49-9=a^2-b^2,\)
\(\displaystyle 40=\frac94 b^2-b^2=\frac54 b^2,\)
\(\displaystyle b^2=32,\)
\(\displaystyle b=4\sqrt2,\)
\(\displaystyle a=\frac32 b=6\sqrt2.\)
Tehát a háromszög keresett oldalai: \(\displaystyle a=6\sqrt2(≈8,4853)\), \(\displaystyle b=4\sqrt2(≈5,6569)\).
Statisztika:
106 dolgozat érkezett. 5 pontot kapott: 82 versenyző. 4 pontot kapott: 8 versenyző. 3 pontot kapott: 3 versenyző. 2 pontot kapott: 4 versenyző. 1 pontot kapott: 5 versenyző. 0 pontot kapott: 4 versenyző.
A KöMaL 2018. márciusi matematika feladatai

