Problem C. 1469. (March 2018)

C. 1469. The foot of the altitude drawn from vertex \(\displaystyle C\) of a triangle \(\displaystyle ABC\) is \(\displaystyle T\), an interior point of side \(\displaystyle AB\). The angle bisector drawn from \(\displaystyle C\) intersects \(\displaystyle AB\) at \(\displaystyle R\). Given that \(\displaystyle AB=10\), \(\displaystyle AT=3\) and \(\displaystyle AR=4\), find the lengths of the sides of the triangle.

(5 pont)

Deadline expired on April 10, 2018.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Használjuk az ábra jelöléseit. \(\displaystyle AB=10\), \(\displaystyle AR=4\), \(\displaystyle AT=3\), ezért \(\displaystyle RB=6\), \(\displaystyle TR=1\) és \(\displaystyle TB=7\). A szögfelező a szemközti oldalt a szomszédos oldalak arányában metszi, ezért \(\displaystyle \frac ab=\frac64=\frac32\). Tehát \(\displaystyle a=\frac32 b\).

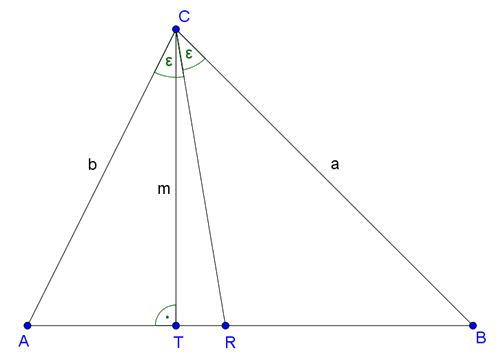
Írjuk fel a Pitagorasz-tételt az \(\displaystyle ATC\) és \(\displaystyle BTC\) derékszögű háromszögekre:

\(\displaystyle m^2+3^2=b^2,\)

\(\displaystyle m^2+7^2=a^2.\)

Vonjuk ki az alsó egyenletből a felsőt és helyettesítsünk be \(\displaystyle a\) helyére \(\displaystyle \frac32 b\)-t:

\(\displaystyle 49-9=a^2-b^2,\)

\(\displaystyle 40=\frac94 b^2-b^2=\frac54 b^2,\)

\(\displaystyle b^2=32,\)

\(\displaystyle b=4\sqrt2,\)

\(\displaystyle a=\frac32 b=6\sqrt2.\)

Tehát a háromszög keresett oldalai: \(\displaystyle a=6\sqrt2(≈8,4853)\), \(\displaystyle b=4\sqrt2(≈5,6569)\).

Statistics:

106 students sent a solution.
5 points:	82 students.
4 points:	8 students.
3 points:	3 students.
2 points:	4 students.
1 point:	5 students.
0 point:	4 students.

Problems in Mathematics of KöMaL, March 2018