 Problem C. 1472. (March 2018)
Problem C. 1472. (March 2018)
C. 1472. A certain game involves collecting cards with various things on them. Each card has exactly two of the following 9 things: colours (red, white, or green), elements (air, earth, fire, or water) and animals (rabbit or sheep). A card shows at most one of each category. In how many different ways is it possible to select four cards such that there are eight different things on them, provided that the game contains all possible combinations?
(5 pont)
Deadline expired on April 10, 2018.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Szemléltessük a lehetséges kártyalapokat egy \(\displaystyle 9\) pontú gráffal, ahol a pontok a kártyán szereplő dolgok (színek, elemek, szereplők), a lehetséges kártyák pedig az élek (1. ábra). A szabályokat figyelembe véve a gráfnak \(\displaystyle 3\cdot4+3\cdot2+4\cdot2=26\) éle van.
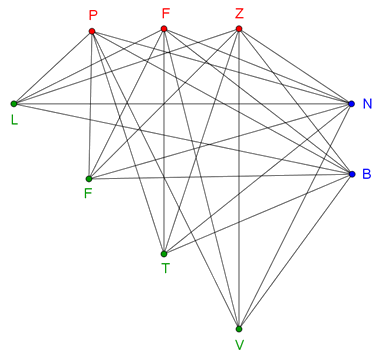
1. ábra
Összesen \(\displaystyle 9\) dolog van. Ha \(\displaystyle 4\) kártyán \(\displaystyle 8\) különböző dolognak kell szerepelnie, akkor pontosan \(\displaystyle 1\) kimarad. Számoljuk össze az eseteket aszerint, hogy milyen dolog marad ki, szereplő, szín vagy elem.
Ha szereplő marad ki, az kétféleképpen történhet. A maradék egy szereplő csak elemmel együtt szerepelhet egy kártyán, mert ha színnel szerepelne, akkor \(\displaystyle 2\) elemnek nem lehetne párt találni (2. ábra).
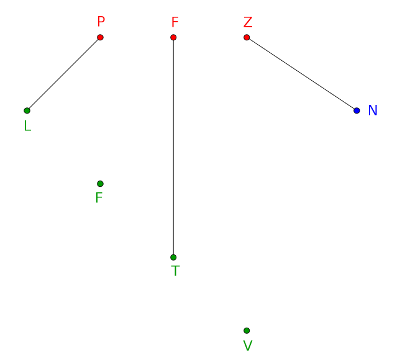
2. ábra
Az egy szereplőnek \(\displaystyle 4\) féle párt találhatunk az elemek közül. A maradék elemek és a színek \(\displaystyle 3!=6\)-féle párt képezhetnek. Így ebben az esetben \(\displaystyle n_{szereplő}=2\cdot4\cdot6=48\)-féleképpen választhatjuk ki a négy kártyát.
Ha szín marad ki, az háromféleképpen történhet. Ha a maradék színek valamelyikét egy szereplővel kötnénk össze (pl. \(\displaystyle FN\), 3. ábra), akkor az elemek közül kettőnek nem tudnánk párt találni.
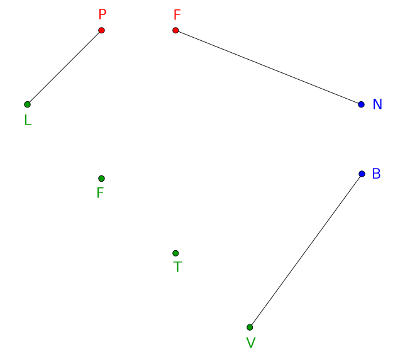
3. ábra
Tehát a \(\displaystyle 4\) elemet a két szín és két szereplő valamelyikével kell összekötni. Ez \(\displaystyle 4!=24\)-féleképpen lehetséges. Így ebben az esetben \(\displaystyle n_{szín}=3\cdot24=72\)-féleképpen választhatjuk ki a négy kártyát.
Végül, ha elemet hagyunk ki, az négyféleképpen történhet. Ilyenkor nem köthetjük mindkét szereplőt színhez, vagy elemhez, mert a maradék szín(ek)ből, illetve elem(ek)ből nem tudnánk párokat képezni (4. ábra).
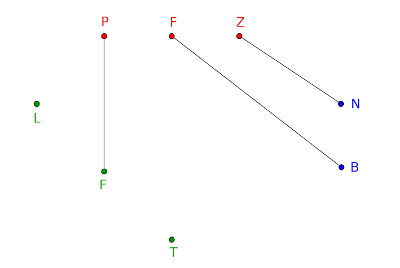
4. ábra
Ezért egyik szereplőt színnel, a másikat pedig elemmel kell összekötnünk. Itt kétféleképpen választhatunk. Az egyik szereplőt a színekkel \(\displaystyle 3\)-, a másikat az elemekkel szintén \(\displaystyle 3\)-féleképpen köthetjük össze. A maradék két színt és két elemet kétféleképpen köthetjük össze. Így ebben az esetben \(\displaystyle n_{elem}=4\cdot2\cdot3^2\cdot2=144\)-féleképpen választhatjuk ki a négy kártyát.
Az összes lehetőségek száma:
\(\displaystyle n_{összes}=n_{szereplő}+n_{szín}+n_{elem}=48+72+144=264.\)
Tehát \(\displaystyle 264\)-féleképpen választhatjuk ki a \(\displaystyle 4\) kártyát úgy, hogy rajtuk \(\displaystyle 8\) különböző dolog legyen.
Statistics:
99 students sent a solution. 5 points: Ács Imre, Agócs Katinka, Almási Adél Csilla, Andó Viola, Antal Réka, Balázs Réka, Biró 424 Ádám, Czett Mátyás, Debreczeni Tibor, Dékány Barnabás, Fodor Marcel, Fonyi Máté Sándor, Gál Bence, Görcs András, Hámori Janka, Hordós Adél Zita, Jankovits András, Jánosdeák Márk, Kerekes Boldizsár, Kinyó Kincső, Kiszelovics Dorina, Koleszár Domonkos, Kovács 157 Zita, Kovács 161 Márton Soma, Kovács 526 Tamás, Kovács Fruzsina Dóra, Markó Gábor, Molnár 410 István, Németh Csilla Márta, Paksi Barnabás, Pinke Andrea, Rassai Erik, Rittgasszer Ákos, Schenk Anna, Shuborno Das, Spányik Teodor, Surján Anett, Szécsi Adél Lilla, Székelyhidi Klára, Szőke Péter, Szőnyi Laura, Ürmössy Dorottya, Vlaszov Artúr, Werner András, Williams Hajna. 4 points: Magyar 257 Boglárka, Wolff Vilmos. 3 points: 12 students. 2 points: 2 students. 1 point: 12 students. 0 point: 24 students. Unfair, not evaluated: 2 solutionss.
Problems in Mathematics of KöMaL, March 2018
