 Problem C. 1474. (March 2018)
Problem C. 1474. (March 2018)
C. 1474. Let \(\displaystyle P\), \(\displaystyle Q\) and \(\displaystyle R\) denote the feet of the altitudes of the acute-angled triangle \(\displaystyle ABC\). Given that \(\displaystyle BP:PA=1:2\) and \(\displaystyle AQ:QC=3:1\), find the proportion of the pieces formed by \(\displaystyle R\) on side \(\displaystyle BC\).
(5 pont)
Deadline expired on April 10, 2018.
Sorry, the solution is available only in Hungarian. Google translation
1. megoldás. Tudjuk, hogy a háromszög magasságvonalai egy pontban metszik egymást (1. ábra), így a hiányzó osztásarány kiszámítására használhatjuk a Ceva-tételt, miszerint
\(\displaystyle \frac{AP}{PB}\cdot\frac{BR}{RC}\cdot\frac{CQ}{QA}=1\)
pontosan akkor igaz, ha az \(\displaystyle AR\), \(\displaystyle BQ\) és \(\displaystyle CP\) egyenesek egy pontban metszik egymást.
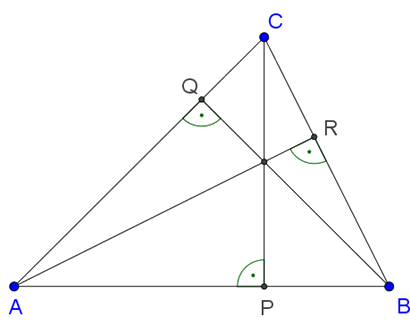
1. ábra
Tudjuk, hogy \(\displaystyle \frac{AP}{PB}=2\) és \(\displaystyle \frac{CQ}{QA}=\frac13\). Ezeket beírva:
\(\displaystyle 2\cdot\frac{BR}{RC}\cdot\frac13=1.\)
Tehát az \(\displaystyle R\) pont osztásaránya:
\(\displaystyle \frac{BR}{RC}=\frac32.\)
2. megoldás. Használjuk a 2. ábra jelöléseit. \(\displaystyle BAR∡=BCP∡=α\), \(\displaystyle CAR∡=CBQ∡=β\), \(\displaystyle ABQ∡=ACP∡=γ\), mert merőleges szárú szögpárok.
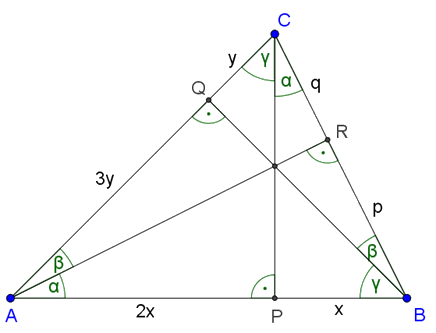
2. ábra
A megadott osztásarányoknak megfelelően legyen \(\displaystyle AP=2x\), \(\displaystyle PB=x\), \(\displaystyle AQ=3y\), \(\displaystyle QC=y\) és legyen \(\displaystyle BR=p\), illetve \(\displaystyle RC=q\).
Fejezzük ki a derékszögű részháromszögekből a jelölt szögek szinuszait kétféleképpen:
| \(\displaystyle (1)\) | \(\displaystyle \sinα=\frac{p}{3x}=\frac{x}{p+q},\) |
| \(\displaystyle (2)\) | \(\displaystyle \sinβ=\frac{q}{4y}=\frac{y}{p+q},\) |
| \(\displaystyle (3)\) | \(\displaystyle \sinγ=\frac{3y}{3x}=\frac{2x}{4y},\) |
amiből \(\displaystyle 2y^2=x^2\), vagyis \(\displaystyle x=\sqrt2 y\). Ezt behelyettesítve az 1. egyenletbe:
\(\displaystyle \frac{p}{3\sqrt2 y}=\frac{\sqrt2 y}{p+q},\)
\(\displaystyle \frac{p}{6y}=\frac{y}{p+q}.\)
Ezt összehasonlítva a 2. egyenlettel:
\(\displaystyle \frac{q}{4y}=\frac{p}{6y}.\)
Amiből a keresett arányt kapjuk:
\(\displaystyle \frac pq=\frac64=\frac32.\)
Statistics:
40 students sent a solution. 5 points: Agócs Katinka, Ajtai Boglárka, Almási Adél Csilla, Balog 518 Lóránd, Bukor Benedek, Deák Péter, Dékány Barnabás, Gálffy Veronika, Gulyás Bálint, Jankovits András, Kiszelovics Dorina, Kovács 161 Márton Soma, Kovács 526 Tamás, Magyar 257 Boglárka, Molnár 410 István, Molnár 921 Ádám, Németh Csilla Márta, Nyitrai Boglárka, Paksi Barnabás, Pszota Máté, Rittgasszer Ákos, Sal Dávid, Spányik Teodor, Surján Anett, Szécsi Adél Lilla, Szőnyi Laura, Tóth Imre, Török Boldizsár. 4 points: Debreczeni Tibor, Pipis Panna, Ruszthi Csilla, Szajkó Szilvia, Wolff Vilmos. 3 points: 4 students. 0 point: 3 students.
Problems in Mathematics of KöMaL, March 2018
