 Problem C. 1475. (March 2018)
Problem C. 1475. (March 2018)
C. 1475. What is the largest possible area of the lateral surface of a cylinder inscribed in a unit sphere?
(5 pont)
Deadline expired on April 10, 2018.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Tekintsük a henger egy tengelymetszetét.
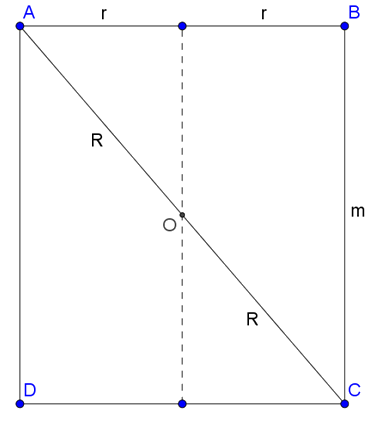
Az \(\displaystyle ABC\) derékszögű háromszögben \(\displaystyle AB=2r\), \(\displaystyle BC=m\) és \(\displaystyle AC=2R\). Tudjuk, hogy \(\displaystyle R=1\). Írjuk fel a Pitagorasz-tételt az \(\displaystyle ABC\) háromszögben:
\(\displaystyle 4r^2=4R^2 - m^2,\)
\(\displaystyle 4r^2=4- m^2.\)
A henger palástjának felszíne: \(\displaystyle A=2rmπ\). A felszín pozitív, így pontosan akkor maximális, ha négyzete is maximális:
\(\displaystyle A^2=4r^2 m^2 π^2=(4-m^2)\cdot m^2 π^2.\)
Legyen \(\displaystyle x=m^2\). Ekkor \(\displaystyle A^2=(4-x)\cdot x\cdot π^2\). Elegendő az \(\displaystyle y=(4-x)\cdot x\) másodfokú függvény maximumát keresni. Képe egy fordított állású parabola, zérushelyei: \(\displaystyle x_1=0\) és \(\displaystyle x_2=4\), tehát a maximum helye \(\displaystyle x=2\). Ez azt jelenti, hogy a henger palástjának felszíne akkor maximális, ha \(\displaystyle m=\sqrt 2\). Ekkor \(\displaystyle 4r^2=4- m^2=2\), vagyis \(\displaystyle r=\frac{\sqrt2}{2}\), \(\displaystyle 2r=\sqrt2\). Látszik, hogy a maximum akkor van, mikor a henger tengelymetszete négyzet. Így a hengerpalást felszínének maximális értéke:
\(\displaystyle A_{max}=2rmπ=2\cdot\frac{\sqrt2}{2}\cdot\sqrt2\cdot π=2π.\)
Statistics:
45 students sent a solution. 5 points: Agócs Katinka, Ajtai Boglárka, Almási Adél Csilla, Balog 518 Lóránd, Bukor Benedek, Deák Péter, Debreczeni Tibor, Dékány Barnabás, Havlik Miklós, Jankovits András, Kis-Tóth Janka, Kiszelovics Dorina, Kovács 111 Bence, Kovács 161 Márton Soma, Kovács 526 Tamás, Lapu Kolos, Molnár 410 István, Molnár 921 Ádám, Németh Csilla Márta, Orbán Balázs Zsolt, Paksi Barnabás, Rittgasszer Ákos, Ruszthi Csilla, Sal Dávid, Spányik Teodor, Surján Anett, Szécsi Adél Lilla, Tierra Coral Luis Geovanny, Varga Dániel Jonatán, Wolff Vilmos. 4 points: Gálffy Veronika, Gulyás Bálint, Szőnyi Laura. 2 points: 4 students. 1 point: 5 students. 0 point: 3 students.
Problems in Mathematics of KöMaL, March 2018
